Review
참고 포스팅 :
2020/12/26 - [Statistics/Time Series Analysis] - [시계열분석] 이동평균법(Moving Average Method)에 의한 분해(1)
[시계열분석] 이동평균법(Moving Average Method)에 의한 분해(1)
안녕하십니까, 간토끼입니다. 이번 포스팅은 최근 M개의 관측치들만을 이용하여 평균을 구하는 방법인 이동평균법에 대해 다뤄보도록 하겠습니다. 이동평균(Moving Average)이란 평활법의 한 종류
datalabbit.tistory.com
안녕하십니까, 간토끼입니다.
이번 포스팅은 지난 포스팅에 이어서 이동평균법에 대해서 좀 더 다뤄보도록 하겠습니다.

지난 포스팅에서 이동평균법에 대한 개념과 단순이동평균법을 이용해 parameter가 한 개인 모형을 추정하는 방법에 대해서 다루었습니다.

즉 상수평균모형과 유사한 형태를 보이는(엄밀히 따지면 parameter가 시간에 따라 변하는 모수라는 점에서 다르죠?) 형태일 때, 이를 추정하는 방법으로 단순이동평균추정량을 제시했었죠.
사실 러프하게 그냥 최근 m개의 데이터만을 이용하여 평균을 냄으로써 미래의 값을 예측한다는 개념이었죠.
그렇기에 이때의 단순이동평균추정량은 당연하게도 불편추정량이 됩니다.
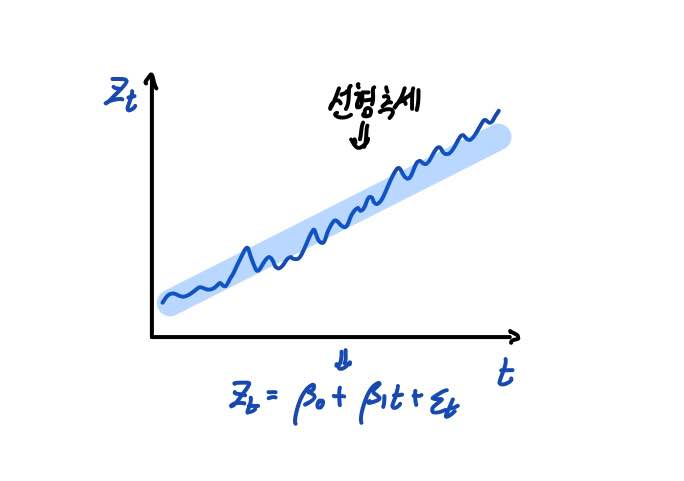
그러나 위와 같이 시계열이 선형추세에 따라 증가하는 경우에도 동일한 방법을 적용할 수 있을까요?
이러한 경우, 위에서 구한 단순이동평균추정량이 다소 부적절할 수 있습니다.
왜 그러한지 한번 보시죠.
한번 시계열이 선형 추세를 따를 때, 단순이동평균추정량을 구해보겠습니다.

유도 과정이 어렵진 않은데 중간에 빨간 밑줄 부분을 처리하는 게 조금은 까다로울 수 있어서 이 부분만 짚고 넘어가보죠.

빨간 부분을 살펴보면 위와 같이 수열의 형태를 보이는 것을 알 수 있습니다.
단순이동평균법은 "m개"의 데이터를 이용하므로, 이를 바탕으로 위와 같이 접근해보면 쉽게 구할 수 있습니다.
자 그래서 위 과정을 통해 보인 식에 Expectation을 씌워 불편성을 만족하는지 살펴보겠습니다.

보시다시피 (m+1)β/2 만큼의 Bias가 항상 발생하는 것을 알 수 있습니다.
즉 단순이동평균추정량을 선형 추세를 따르는 시계열의 n+1 시점의 자료의 예측값으로 사용하면 항상 (m+1)β/2 만큼의 Bias가 생기게 됩니다.
이러한 문제를 해결하기 위해서는 좀 더 다른 방법을 이용해 접근해볼 필요가 있습니다.
언젠가 비슷한 문제에 당면한 적이 있었던 것 같은데요.
맞습니다!
선형 추세를 따르는 시계열에 단순지수평활을 적용할 때 비슷한 문제를 겪었었죠 ㅎㅎ
그래서 이에 대한 해결책으로 이중지수평활을 적용함으로써 모형의 parameter 2개를 추정하였습니다.
[시계열분석] 이중지수평활법(Double Exponential Smoothing Method)
Review 참고 포스팅 : 2020/11/16 - [Statistics/Time Series Analysis] - [시계열분석] 단순지수평활법(Simple Exponential Smoothing Method) [시계열분석] 단순지수평활법(Simple Exponential Smoothing Method..
datalabbit.tistory.com

자 그래서 마찬가지로 단순이동평균 추정량의 단순이동평균 추정량을 구함으로써 모형의 parameter를 추정해 이 추정량을 이용합니다.
즉 단순이동평균추정량 M(1)을 예측값으로 이용하지 않고,
M(1)과 M(1)의 단순이동평균 M(2)를 같이 구하고, 이 두 추정량을 이용해 β0, β1의 추정량을 구합니다.
그리고 이 추정량을 선형추세모형에 대입하여 예측값을 구하면 되겠죠.
한번 차근차근 살펴보겠습니다.

먼저 M(1)의 단순이동평균추정량인 M(2)를 유도해보도록 합시다.
과정 자체는 위에서 했던 유도 과정과 크게 다르지는 않아서 깊게 설명은 하진 않겠습니다.
또한 모형의 오차항인 엡실론은 그냥 생략했습니다. 어차피 기댓값 씌우면 사라지니깐요.

그래서 기댓값을 씌우면 mβ 만큼의 Bias가 남아있긴 합니다.
어쨌든 2개의 미지수에 대한 식이 2개니 이 단순이동평균추정량 공식을 이용해 beta들에 대한 식으로 나타낼 수 있겠죠!
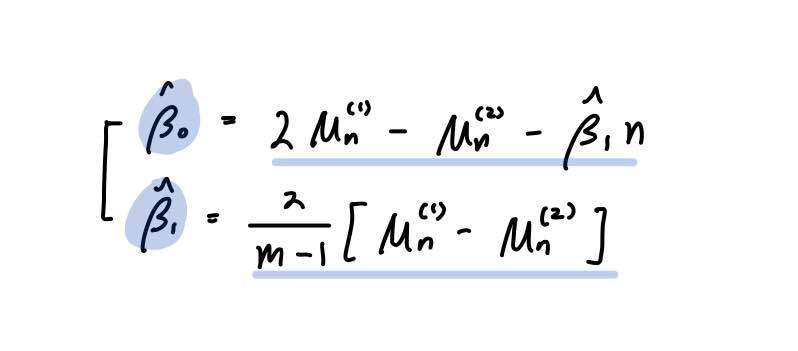
추정량을 구하면 다음과 같습니다.
그래서 이 추정량들을 기존 선형추세모형 식에 대입하여 예측값을 구해보도록 하죠.
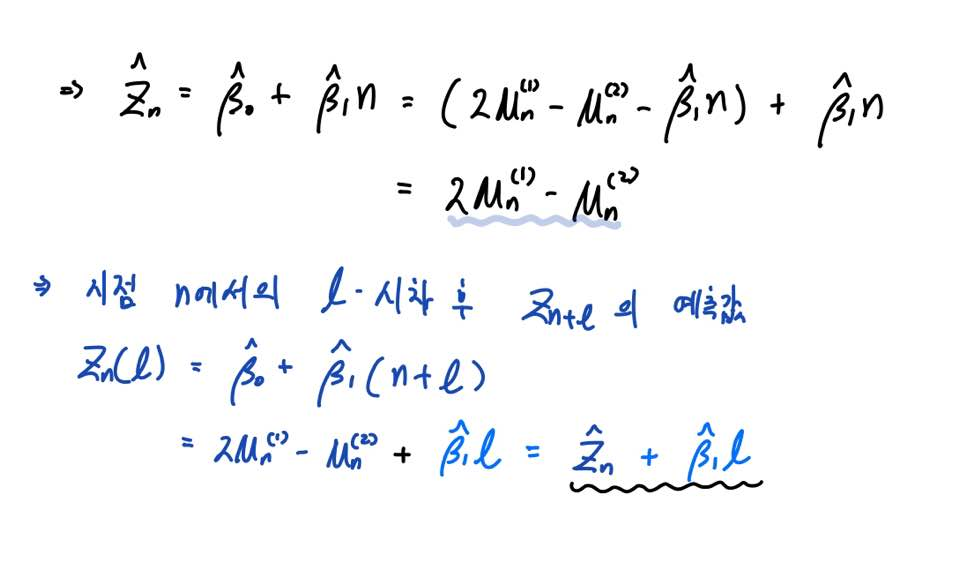
즉 시점 n의 예측값은 2M(1) - M(2)가 됨을 알 수 있으며,
이를 바탕으로 시점 n에서의 l-시차 후 예측값은 n-시점의 예측값에 l-시차만큼의 증가된 값을 더하는 거라고 이해하면 되겠죠.
사실 이동평균법은 예측의 목적보다는 성분을 분리하고자 할 때 많이 사용하는 방법입니다.
그렇기에 예측의 개념이 다소 와닿지 않으실 수는 있어요... ^^
저도 썩 매력적으로 다가오진 않네요.
다음 포스팅에서는 이동평균법을 이용한 계절조정에 대해서 좀 더 다뤄보고,
예측을 위한 중요한 개념인 확률과정(Stochastic Process)와 ARIMA를 위해 얼른 넘어가도록 하겠습니다.
감사합니다.
잘 읽으셨다면 게시글 하단에 ♡(좋아요) 눌러주시면 감사하겠습니다 :)
(구독이면 더욱 좋습니다 ^_^)
- 간토끼(DataLabbit)
- University of Seoul
- Economics & Data Science
'Statistics > Time Series Analysis' 카테고리의 다른 글
| [시계열분석] 정상성(Stationarity) (2) | 2021.07.04 |
|---|---|
| [시계열분석] 확률과정(Stochastic Process) (0) | 2021.02.02 |
| [시계열분석] 이동평균법(Moving Average Method)에 의한 분해(1) (0) | 2020.12.26 |
| [시계열분석] 추세모형에 의한 분해법 (2) | 2020.12.23 |
| [시계열분석] 이중지수평활법(Double Exponential Smoothing Method) (0) | 2020.11.17 |
