안녕하십니까, 간토끼입니다.
이번 포스팅에서는 전치행렬(Transposed Matrix)의 개념에 대해서 다뤄보겠습니다.

전치행렬이란 임의의 행렬 A가 주어졌을 때, 그 행렬의 행과 열을 바꾸어 얻어낸 행렬을 의미합니다.
즉 행렬 A가 3x2 사이즈의 행렬이라고 가정하면, 전치행렬 AT는 2x3 사이즈의 행렬이 됩니다.

행렬 A의 열벡터가 [2,5,1]T, [3,0,1]T 이죠?
이를 전치(Transpose)하면 행벡터인 [2,5,1], [3,0,1]로 바뀌게 됩니다.
마찬가지로 기존의 행벡터 [2,3], [5,0], [1,1] 이 전치하면 열벡터로 바뀌게 되겠죠.
이러한 의미에서 행과 열을 바꾸어 얻어낸다고 하는 것입니다.
만약 행렬의 사이즈가 nxn으로 같은 Square Matrix라면 어떨까요?
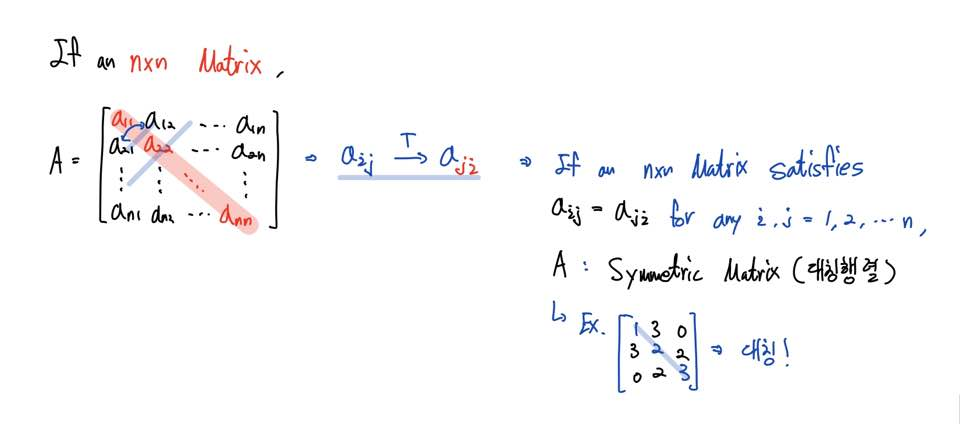
행렬의 사이즈가 같다면 대각성분을 기준으로 바뀌게 되겠죠. 상상하기 더욱 쉬울 것입니다.
이때 만약 임의의 i, j (i,j = 1, 2, ..., n)에 대해서 a(i,j) = a(j,i) 이 성립한다면 전치하여도 기존의 행렬과 전치행렬이 같을 것입니다.
이를 대칭행렬(Symmetric Matrix)라고 합니다.
그리고 전치행렬은 다음과 같은 성질을 가집니다.
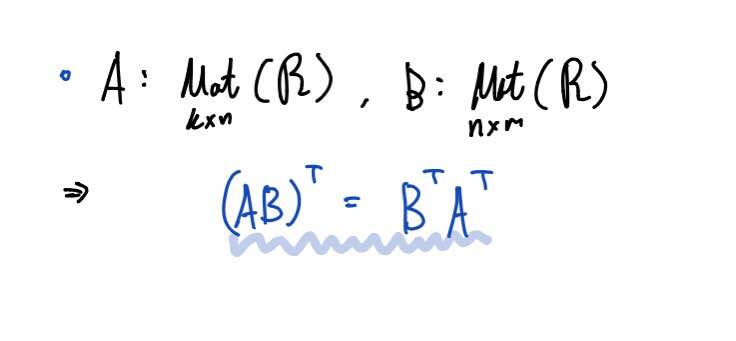
임의의 k x n 행렬 A와 n x m 행렬 B에 대하여 다음과 같이 전치가 성립합니다.
k x n, n x m 이라고 가정한 것은 두 행렬의 곱 연산이 가능하다는 것을 전제하기 위해서 입니다.

만약 행렬이 늘어나도 곱 연산이 가능하다면 이렇게도 가능합니다.
아직 다루지는 않았는데 역행렬이란 친구도 전치행렬처럼 우측 상단에 기호를 취하고 있습니다.
간단한 증명을 한번 보시죠.
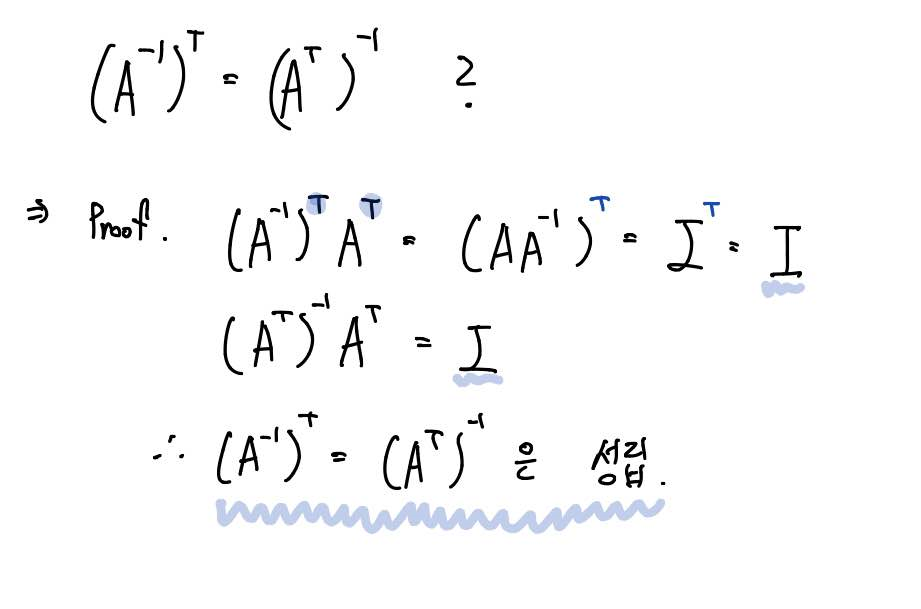
어려운 증명은 아닌데, 역행렬의 전치와 전치행렬의 역행렬이 같은지 증명하는 문제입니다.
등식의 우항을 보면 전치행렬의 역행렬이 있으므로 전치행렬을 곱해주면 Identity Matrix가 되는 것은 자명합니다.
따라서 좌변에도 전치행렬을 곱해줌으로써 Identity Matrix가 되는지를 보이면 되겠죠.
어려운 개념은 아니라 가볍게 다뤘습니다만, 앞으로 전치 기호는 자주 나올 겁니다.
특히 열벡터는 세로로 길쭉하기에 칠판이나 설명서에 표기하기가 어려워, 행벡터 꼴의 전치 형태로 항상 표현하곤 합니다.
앞으로 선형대수든, 통계학이든, 머신러닝-딥러닝이든 그러한 표기법이 자주 등장하니,
아~ 열벡터를 Transpose한 거구나~ 라고 이해하시면 됩니다.
(가끔 표기법에 익숙하지 않은 분들이 벡터의 T제곱이라고 하는 걸 들은 적이 있어서... ㅋㅋㅋㅋㅋ)
다음 포스팅에서는 행렬식(Determinant)에 대해서 다뤄보겠습니다.
감사합니다.
잘 읽으셨다면 게시글 하단에 ♡(좋아요) 눌러주시면 감사하겠습니다 :)
(구독이면 더욱 좋습니다 ^_^)
- 간토끼(DataLabbit)
- University of Seoul
- Economics, Big Data Analytics
'Statistics > Matrix Algebra' 카테고리의 다른 글
| [행렬대수학] 행렬식(Determinant) 2 - 행렬식의 유용한 성질과 수반행렬(Adjoint) (1) | 2023.11.01 |
|---|---|
| [행렬대수학] 행렬식(Determinant) 1 - 행렬식의 개념 (8) | 2020.09.05 |
| [행렬대수학] 행렬과 사상 (4) | 2020.07.23 |
| [행렬대수학] 행렬 대수(Matrix Algebra) (0) | 2020.07.17 |
| [행렬대수학] 가우스-조던 소거법(Gauss-Jordan Elimination) (2) | 2020.07.01 |
