Review
참고 포스팅 :
2020/06/28 - [Statistics/Matrix Algebra] - [행렬대수학] 가우스 소거법(Gaussian Elimination)
[행렬대수학] 가우스 소거법(Gaussian Elimination)
Review 참고 포스팅 : 2020/06/28 - [Statistics/Matrix Algebra] - [행렬대수학] 행렬대수학(Matrix Algebra) 기초 - 행렬(Matrix) [행렬대수학] 행렬대수학(Matrix Algebra) 기초 - 행렬(Matrix) 안녕하십니까,..
datalabbit.tistory.com
안녕하십니까, 간토끼입니다.
지난 포스팅에서는 linear system에서 방정식의 해를 구하는 방법인 가우스 소거법(Gaussian Elimination)에 대해서 다뤄봤습니다.
이번에는 보다 직관적으로(?) 해를 구할 수 있는 방법인 가우스-조던 소거법(Gauss-Jordan Elimination)에 대해 다뤄보겠습니다.

가우스 조던 소거법, 다른 말로는 조르단, 요르단 등 책의 표기법에 따라 약간씩은 다른데요.
저는 대충 표준적으로 부르는 방식인 가우스 조던 소거법이라고 하겠습니다.
우리가 가우스 소거법을 통해 얻어낸 모양은 행 사다리꼴 행렬(Row Echelon Form of Matrix)이었는데요.
가우스 조던 소거법은 행 사다리꼴 행렬을 기약 행 사다리꼴 행렬(Reduced Row Echelon Form of Matrix)로 바꿔주는 방법론이라고 이해하시면 됩니다.
그나저나 기약 행 사다리꼴이라고 하니 좀 직관적이지가 않습니다. 특히 선형대수를 공부하다보면 영어 표현이 더욱 편할 때가 있습니다.
(추후 다룰 nonsingular -> 정칙행렬 등)과 같이 생전 들어본 적도 없는 한국어 표현으로 번역한 게 많아서... 그냥 영어 표현을 섞어 쓰겠습니다.
각설하고 기약 행 사다리꼴은 행렬의 대각성분을 1로 만들어주고, 대각성분을 제외한 나머지 성분은 0으로 이루어진 행렬을 의미합니다.
구하는 과정은 가우스 소거법과 마찬가지로 기본 행 연산을 이용하면 됩니다.
같이 보시죠.

먼저 3행의 대각성분이 -1인 게 마음에 안 들어서 3행에 -1을 곱해주었습니다.
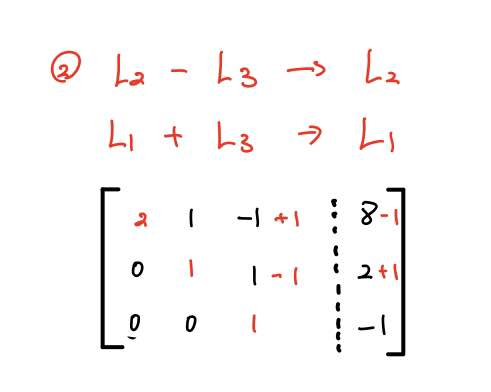
이후 기약 행 사다리꼴의 정의(이하 'RREF')에 따라 대각성분(3행, 3열)을 제외한 3열의 나머지 성분을 0으로 만들어주기 위해 기본 행 연산을 이용하여 각각 빼주고 더해줍니다.

대각성분을 제외한 3열의 나머지 부분이 모두 0이 된 것을 알 수 있죠.
마찬가지로 2열의 대각성분을 제외한 나머지 부분도 0으로 만들어주기 위해 1행에 2행을 빼줍니다.
그러면 1행은 [2 0 0 | 4] 가 됩니다.

마지막으로 RREF의 정의에 따라 대각성분을 1로 만들어주기 위해 2로 나눠줍니다.
짜잔 깔끔한 형태가 되었네요!

이러한 형태의 좋은 점은 linear system의 해를 단숨에 구할 수 있다는 것입니다.
기존 가우스 소거법에서 도출한 행 사다리꼴 행렬(이하 'REF')에서는 후진대입법을 이용하여 일일이 대입한 후, 방정식을 풀어야했지만, RREF는 깔끔하게 각 해에 대한 성분만 상수항에 대응되므로, 바로 해를 구할 수 있습니다.
물론 예시로 든 문제는 굉장히 풀기 편한 문제입니다. 실제로는 복잡하고 더러운 문제도 많겠죠?

다시 한번 RREF를 살펴보면, 대각성분을 1로 만들어주고, 대각성분을 제외한 나머지 성분은 0이 됨을 알 수 있습니다.
그래서 기약(Reduced)라는 수식어가 붙은 것임을 이해하시면 좋을 것 같습니다.

우리는 행렬의 행의 개수(n)와 열의 개수(m)이 같은 행렬을 정방행렬(Square Matrix)라고 합니다.만약 정방행렬의 RREF가 다음과 같다면, 이를 단위행렬(Identity Matrix)라고 부릅니다.
이때 위 행렬에서 pivot(각 행에서 처음으로 0이 아닌 상수가 나오는 성분)의 개수는 3개인데요.행렬에서 이 pivot의 개수를 우리는 rank라고 부릅니다.
즉, 위 행렬을 A라고 한다면, rank(A) = 3이라고 할 수 있죠.
지금은 가볍게 랭크가 무엇인지 살짝만 짚고 넘어갔는데, 나중에 선형공간을 다룰 때 rank는 큰 의미를 지닙니다. 추후 다뤄보도록 하죠.
다음 포스팅에서는 행렬의 몇 가지 형태와, 기본 용어에 대해서 좀 더 다뤄보도록 하겠습니다.
감사합니다.
잘 읽으셨다면 게시글 하단에 ♡(좋아요) 눌러주시면 감사하겠습니다 :)
(구독이면 더욱 좋습니다 ^_^)
- 간토끼(DataLabbit)
- University of Seoul
- Economics, Big Data Analytics
'Statistics > Matrix Algebra' 카테고리의 다른 글
| [행렬대수학] 전치행렬(Transposed Matrix) (1) | 2020.09.04 |
|---|---|
| [행렬대수학] 행렬과 사상 (4) | 2020.07.23 |
| [행렬대수학] 행렬 대수(Matrix Algebra) (0) | 2020.07.17 |
| [행렬대수학] 가우스 소거법(Gaussian Elimination) (2) | 2020.06.28 |
| [행렬대수학] 행렬대수학(Matrix Algebra) 기초 - 행렬(Matrix) (0) | 2020.06.28 |
