Review
참고 포스팅 :
2020/07/17 - [Statistics/Matrix Algebra] - [행렬대수학] 행렬 대수(Matrix Algebra)
[행렬대수학] 행렬 대수(Matrix Algebra)
안녕하십니까, 간토끼입니다. 지난 포스팅에서는 선형 시스템(Linear System) 하에서 방정식의 해를 구할 수 있는 방법인 가우스 소거법, 가우스 조던 소거법에 대해서 다루었습니다. 이번에는 행렬
datalabbit.tistory.com
안녕하십니까, 간토끼입니다.
지난 포스팅에서는 다양한 행렬의 연산에 대해서 다루었습니다.
다른 건 무난하게 생각해도 무방하나, 행렬의 곱은 연산에 있어서 차원을 고려해야 하므로 주의해야 한다고 말씀드렸습니다.
이번 포스팅에서는 이 행렬의 곱에 대해서 조금 더 다뤄보도록 하겠습니다.

앞서 살펴본 행렬 대수, 즉 다양한 행렬의 연산에 대해 살펴보면 행렬은 우리가 일반적으로 실수에 대해서 연산하던 것과 크게 다르지 않았습니다.
덧셈, 상수배가 가능하고, 교환-분배-결합법칙 등이 성립하던 것처럼 말이죠.
다시 말해서 이러한 것도 가능하겠습니다.
벡터 x와 y, 그리고 z가 있다고 가정하고 z = x + y 라는 관계를 정의하겠습니다.
이때 임의의 행렬 (단, 행렬곱에 있어 차원의 문제는 없다고 가정) A를 벡터 z에 곱해주면
당연히 Az = Ax + Ay가 성립할 것입니다.
마찬가지로 임의의 스칼라 c에 대한 스칼라곱 y = cx 에 대해서도 행렬 A를 y에 곱해주면
Ay = c(Ax)가 성립합니다.
이처럼 행렬 A는 정의한 벡터의 덧셈과 스칼라곱을 유지해주는 기법이라고 할 수 있습니다.
여기서 선형 사상의 개념을 '간략히' 짚고 넘어가겠습니다.

임의의 n차원 벡터 x, y가 있고 스칼라 c가 있다고 가정하면,
이에 대해 다음 성질을 만족하는 f를 선형 사상(Linear Mapping)이라고 정의합니다.
이 정의를 이용하면 행렬 A를 곱한다는 사상은 선형 사상이라고도 할 수 있습니다.
왜 그런지 한번 살펴보시죠.

다음과 같은 선형 시스템이 있다고 가정합시다.
이는 아래와 같이 행렬, 벡터를 이용하여 표기할 수 있습니다.

잘 생각해보면 y와 x는 벡터인데 각 계수로 이루어진 A는 행렬입니다.
즉 벡터 x와 행렬 A가 만나서 y라는 벡터가 만들어지는 구조인 거죠.

음... 뭔가 중학교 때부터 익숙하게 보던 그림이 보입니다.
이런 구조를 한번 생각해보도록 하죠.
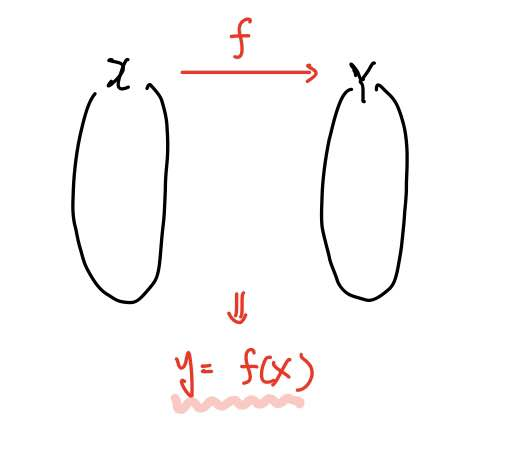
우리가 사상이라는 말을 크게 듣지는 않았으나, '함수 f'를 이용하여 다음과 같은 구조로 도식화하는 것은 중학교 때부터 자주 보았습니다.
함수의 형태에 따라 일대일 대응이니 뭐니 하면서 이러한 구조로 나타냈었죠.
이 구조를 가만히 살펴보면, f(x)라는 것의 의미는 변수 x를 f라는 함수에 넣어 y라는 값으로 보내준다고도 이해할 수 있을 것 같습니다.
즉 함수 f는 변수 x와 y를 이어주는 징검다리같은 역할이 되는 셈이죠!
자 다시 행렬 구조로 돌아가보죠.

변수 x, y를 벡터라고 하고 함수 f 대신 행렬 A로 정의하면,
위 선형 시스템은 벡터 x가 행렬 A에 의해 벡터 y로 보내지는 구조라고 말할 수 있습니다!
이러한 의미에서 행렬은 사상이라고 하는데, 자세한 내용은 추후 선형변환의 개념을 다루면서 짚고 넘어갈 계획입니다.
결론은 n차원 벡터 x에 m x n 행렬 A를 곱하면, m차원 벡터 y = Ax 가 얻어집니다.
즉 임의의 행렬 A를 지정하면 한 벡터를 다른 벡터에 옮기는 사상이 결정되는 것이라고 할 수 있으며,
다시 말해서 행렬은 n차원 공간(벡터 x)에서 m차원 공간(벡터 y)이라는 다른 세계에 옮기는 것이라고도 할 수 있습니다.
이번에는 좀 더 확장해서 행렬 간의 곱, 사상의 합성에 대해서 정의해보겠습니다.
먼저 우리가 쉽게 접했을만한 함수의 합성에 대해서 살펴보도록 하죠.

다음과 같이 f : X -> Y 인 함수 f와 g: Y -> Z인 함수 g가 있다고 가정합시다.
그러면 함수 g와 f의 합성함수인 g◦f(x)는 다음과 같이 g(f(x)) 라고 할 수 있으며,
이는 3(2x)^2로 표현할 수 있습니다.
행렬 간의 곱도 이렇게 합성함수마냥 사상의 합성으로서 정의할 수 있습니다.

k x m 행렬 B와 m x n 행렬 A의 곱인 BA를 다음과 같이 정의해보죠.
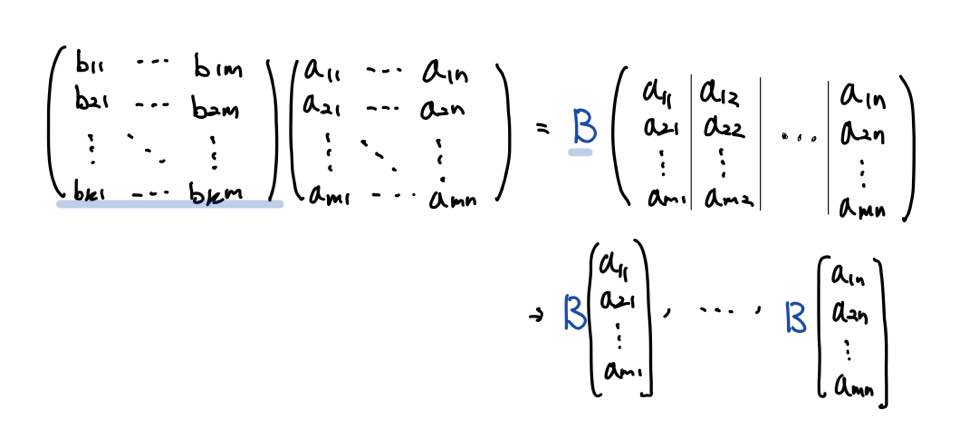
행렬곱 BA는 다음과 같이 행렬 B와 A의 열벡터(Column Vector)간의 곱으로써 행렬곱 BA의 열벡터를 표현할 수 있습니다.
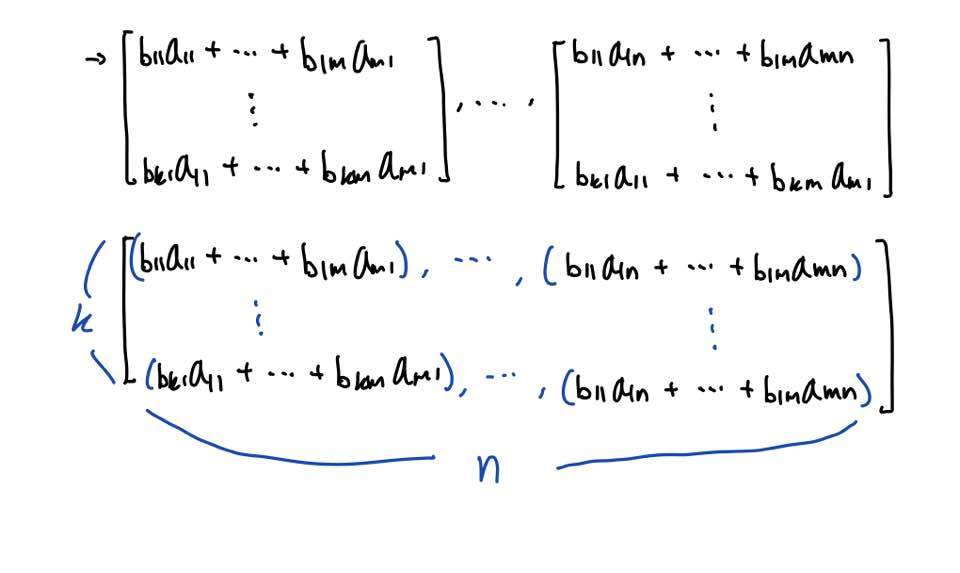
이 행렬 B와 A의 열벡터 간의 곱을 쭉 전개해보면 다음과 같이 최종적으로 k x n 행렬이 얻어지는 것을 알 수 있습니다.
그래서 이 행렬 BA는 무슨 역할이냐,
위에서 정의한 합성함수처럼 행렬도 비슷하게 꾸며봅시다.
y = Ax 라는 선형시스템과 z = By 라는 선형시스템을 정의하면,
기본적으로 벡터 x가 사상(행렬) A에 의해 벡터 y가 되고, 이 벡터 y는 사상(행렬) B에 의해 벡터 z가 되겠죠.

즉 최종 목적지는 z = By = B(Ax)가 될 것이며, 행렬의 결합법칙에 의해 z = (BA)x 라고 할 수 있습니다.
다시 말해서 행렬 BA는 벡터 x를 벡터 z로 보내주는 사상이라는 거죠!
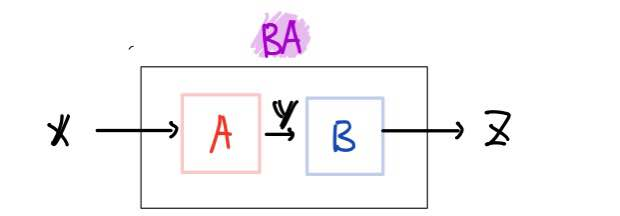
즉 벡터 x에 A하고 B하면 벡터 z가 되는데, 이때 A하고 B한다는 AB가 아니라 BA가 됩니다.
헷갈릴 수는 있는데, 이러한 맥락을 잘 기억하시면 됩니다.
사실 여기서 선형 사상을 다루기엔 시기상조인데 개념 정리도 할 겸 '간단하게' 다뤄보았습니다.
다음엔 행렬의 다양한 종류를 살펴보면서 점점 개념을 확장해보겠습니다.
감사합니다.
잘 읽으셨다면 게시글 하단에 ♡(좋아요) 눌러주시면 감사하겠습니다 :)
(구독이면 더욱 좋습니다 ^_^)
- 간토끼(DataLabbit)
- University of Seoul
- Economics, Big Data Analytics
'Statistics > Matrix Algebra' 카테고리의 다른 글
| [행렬대수학] 행렬식(Determinant) 1 - 행렬식의 개념 (8) | 2020.09.05 |
|---|---|
| [행렬대수학] 전치행렬(Transposed Matrix) (1) | 2020.09.04 |
| [행렬대수학] 행렬 대수(Matrix Algebra) (0) | 2020.07.17 |
| [행렬대수학] 가우스-조던 소거법(Gauss-Jordan Elimination) (2) | 2020.07.01 |
| [행렬대수학] 가우스 소거법(Gaussian Elimination) (2) | 2020.06.28 |
