Review
참고 포스팅 :
2021.07.05 - [Statistics/Time Series Analysis] - [시계열분석] 백색잡음과정(White Noise Process)
[시계열분석] 백색잡음과정(White Noise Process)
Review 참고 포스팅 : 2021.07.04 - [Statistics/Time Series Analysis] - [시계열분석] 정상성(Stationarity) [시계열분석] 정상성(Stationarity) Review 참고 포스팅 : 2021.02.02 - [Statistics/Time Series An..
datalabbit.tistory.com
안녕하십니까, 간토끼입니다.
지난 포스팅에서 정상 시계열의 대표적인 예인 백색잡음과정에 대해 다루었다면,
이번 포스팅에서는 비정상 시계열의 예인 확률보행과정(Random Walk Process)에 대해 다뤄보겠습니다.

확률보행과정(Random Walk Process)

확률보행과정(Random Walk Process)이란 ε ~ WN(0, σ^2) 일 때 위와 같이 정의되는 확률과정을 의미합니다.
크게 절편(Drift)이 있는 경우와 그렇지 않은 경우로 나눠볼 수 있는데요.
왜 '확률보행'이라는 이름이 붙었는지 한번 보시죠.

이 백색잡음과정을 따르는 ε_t 을 시점 t에서 어떤 사람이 임의의 방향으로 움직이는 보폭으로 한번 정의해보죠.

말 그대로 랜덤(Random)한 값입니다.
가만히 서있는 사람이 다음 발걸음을 어느 방향으로 내딛긴 할텐데, 정확히 어디로 내딛을지 모르는 상황입니다.
다만 현재 서있는 지점을 원점(0)이라고 할 때, 우측으로 간다면 양(+)의 값을 갖고 좌측으로 간다면 음(-)의 값을 갖는다고 방향에 따른 부호만 정의해보죠.
만약 X-Y 좌표축에 표시할 경우 위로 가면 양(+), 아래로 가면 음(-)이 되겠죠?

처음 원점을 0이라고 할 때, t =1, 2, ... 에 따라 전개해보면 위와 같습니다.
결국 t 시점의 자료값 Z_t 는 t개의 ε을 다 더한 것과 같죠.
즉 랜덤워크에서 Z_t 는 't-시간 후의 위치'를 의미합니다.
사람 한 명이 막 랜덤하게 걷다보면 어디로 갈까 ~ 뭐 이런 의미죠.
매시점마다 ε는 발걸음을 의미하고, 그 발걸음이 모이다보면 어느 위치에 도달하게 되잖아요? 그게 Z_t가 됩니다.
아무튼 이 확률보행과정, 임의보행과정 혹은 랜덤워크라고 불리는 이 확률과정은 Covariance Stationarity를 만족하는 시계열일까요?
Covariance Stationarity 는 기댓값과 분산이 t와 무관한 상수이고, 공분산은 시점 t가 아닌 시차 k에 관한 함수여야 한다고 했죠.
2021.07.04 - [Statistics/Time Series Analysis] - [시계열분석] 정상성(Stationarity)
[시계열분석] 정상성(Stationarity)
Review 참고 포스팅 : 2021.02.02 - [Statistics/Time Series Analysis] - [시계열분석] 확률과정(Stochastic Process) [시계열분석] 확률과정(Stochastic Process) 안녕하십니까, 간토끼입니다. 이번 포스팅은 확..
datalabbit.tistory.com
한번 기댓값부터 따져보겠습니다.
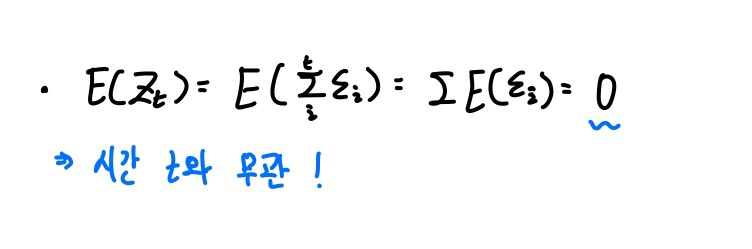
먼저 기댓값은 0이 되므로 시간 t와 무관합니다.

그러나 분산, 공분산 모두 시간 t의 함수입니다.
그러므로 정상 시계열이라고 할 수 없습니다. 비정상(NonStationary)시계열이죠.

그려보면 이렇게 생겼습니다.
다음은 절편(Drift)이 있는 랜덤워크에 대해 다뤄보죠.

달라진 건 상수항이 추가됐다는 것입니다.
전개해보면 상수항에 시간 t가 곱해진 꼴이 추가가 된 것을 알 수 있습니다.

마찬가지로 기댓값, 분산이 시간 t의 함수이므로 Covariance Stationarity의 정의를 만족할 수 없습니다.
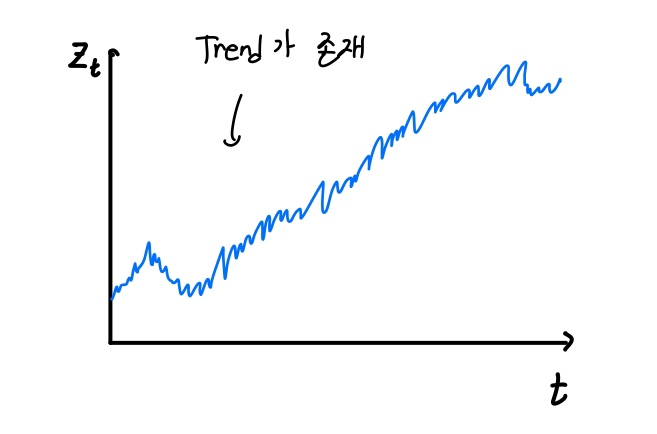
절편이 없는 랜덤워크와 다른 점은 Trend가 존재합니다.
시간의 흐름에 따라 증가하는 형태임을 알 수 있습니다.
다음 포스팅은 시계열자료의 특성을 나타내는 중요한 지표 중 하나인 자기상관함수에 대해 다뤄보도록 하겠습니다.
감사합니다.
잘 읽으셨다면 게시글 하단에 ♡(좋아요) 눌러주시면 감사하겠습니다 :)
(구독이면 더욱 좋습니다 ^_^)
- 간토끼(DataLabbit)
- University of Seoul
- Economics & Data Science
'Statistics > Time Series Analysis' 카테고리의 다른 글
| [시계열분석] 부분자기상관함수(Partial Autocovariance Function, PACF) (2) | 2021.07.14 |
|---|---|
| [시계열분석] 자기상관함수(AutoCovariance Function; ACF) (0) | 2021.07.12 |
| [시계열분석] 백색잡음과정(White Noise Process) (0) | 2021.07.05 |
| [시계열분석] 정상성(Stationarity) (2) | 2021.07.04 |
| [시계열분석] 확률과정(Stochastic Process) (0) | 2021.02.02 |
