안녕하십니까, 간토끼입니다.
이번 포스팅은 유한개의 설명변수의 Lagged Variable을 이용하여 반응변수 y를 예측하는 모형인 Finite Distributed Lag Model, 줄여서 FDL Model에 대해 다뤄보도록 하겠습니다.

Finite Distributed Lag Model(이하 FDL Model)은 유한시차분포모형(?)이라고 번역이 되는 것 같습니다.
t-시점의 자료 X_t가 있을 때, t-시점보다 이전 시점(t-1, t-2, ..., 2, 1)의 자료를 Lagged Variable이라고 부릅니다.
그리고 이러한 시차를 Lag라고 부릅니다.
즉 X_t의 Lag = 1인 변수는 X_t-1 이 되겠죠.
그래서 이러한 Lagged Variable이 q개 있다고 가정하면, q차 유한시차분포모형이 됩니다.
이름이 너무 거창하네요. 그냥 FDL Model이라고 하죠.

그래서 이러한 FDL Model은 반응변수 y를 예측할 때 설명변수의 Lagged Variable을 이용하는 것이 특징입니다.
아무래도 이전 포스팅에서 다루었던 Static Model은 동시대적인 관계만을 파악했었는데,
시계열 자료의 특성상 과거의 값이 미래에 영향을 줄 수 있다는 점에서 Static Model은 다소 약한 모형일 수 있습니다.
예를 들어 정부가 기준 금리를 s-시점에서 인상했다면, 이로 인한 경제의 여파가 즉각적으로 나타날 수 있을까요?
아니겠죠. 경제주체들이 그 현상을 인지하고, 이에 대한 대응을 하기까지 시간이 다소 걸릴 겁니다.
그리고 여러 경제주체 간의 연쇄효과가 나타나는 것은 더욱 오래 걸릴 것이고요.
그렇기에 오히려 동시대적인 관계에서 나타나는 효과보다 과거에서 미래에 영향을 주는 효과가 더욱 클 것으로 보는 게 더욱 합리적일 것입니다.
그렇다면 이러한 여파가 어떻게 미치는지 한번 예시를 통해 살펴보도록 하죠.
앞으로 드는 예시는 쉬운 이해를 위해 오차항이 0인 q차 FDL Model을 가정하겠습니다.

현재 시점인 t-시점이 아닌 모든 시점 s의 값은 상수 c이며, 현재 시점인 t-시점에만 c+1로 변화가 일어났다고 가정하겠습니다.
즉 위에서 보시다시피 t-시점에서의 설명변수 Z_t의 값이 c+1로 되어있죠.

이때 시간이 지날수록 c+1의 값은 점점 과거가 되겠죠.
그리고 이러한 시간이 q만큼 지나면, Z_(t-q)의 값이 c+1이 될 겁니다.
그리고 q+1만큼 시간이 지나면 t-시점에서 c+1의 값을 가졌던 건 모형에서 사라지게 되겠죠.

이때 t-시점에서 c가 아닌 c+1이 됐으니 1만큼 값이 커진 거잖아요?
즉 t-시점에서 설명변수 Z가 1단위 증가함에 따라 반응변수 y의 변화를 측정한 것을 Impact Propensity라고 합니다.
쉽게 말하면 모든 시점에서 동일한 값을 갖다가 어떠한 정책, 혹은 특정한 변화가 t-시점에 일어났을 때, 이러한 변화가 미치는 영향력을 측정한 것이라고 이해할 수 있겠죠.

그리고 t-시점의 변화가 j-period 동안 어떠한 변화를 가져왔는지 측정하면
t+j 시점의 관측값 Y_(t+j)에서 t-1 시점의 관측값 Y_(t-1)을 빼면 j만큼의 시간 동안 발생한 변화를 알 수 있겠죠.
그렇다면 이번엔 t-시점 이후로 쭉 변화가 발생하는 상황을 가정해보죠.
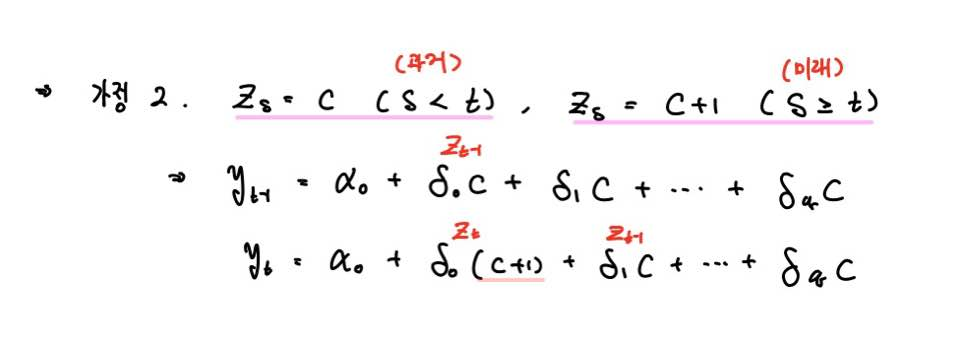
현재 t-시점 이전의 과거에는 상수 c의 값을 갖다가 t-시점 이후부터 c+1의 값을 갖는 상황입니다.
즉 일시적인 변화가 아닌 지속적인 변화가 되는 것이죠.

그렇기에 t-시점부터 점점 변화가 누적되어 t+q 시점이 되면 모든 설명변수의 값이 c+1이 됩니다.
그리고 이러한 변화가 계속 이어져 Z_(s) = c 인 값을 찾아볼 수 없게 됩니다.
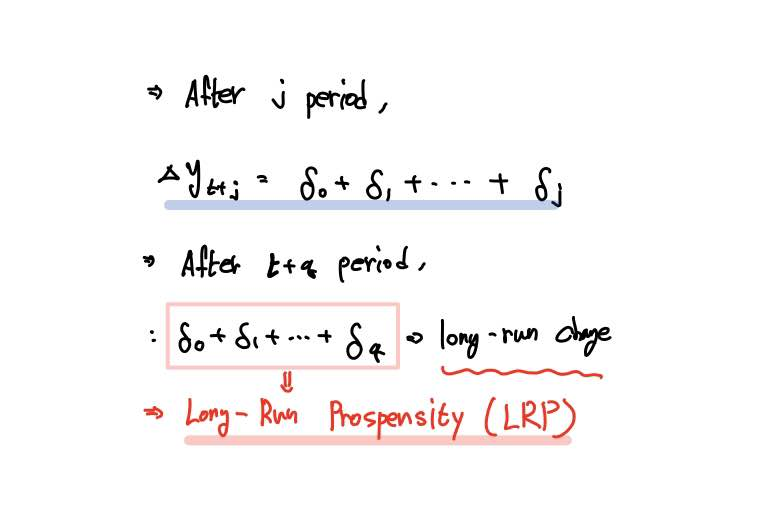
이때 위 impact propensity와 마찬가지로,
t+q만큼 시간이 지났을 때의 회귀계수들은 q개 있을 것이며,
이를 다 더한 것을 Long-Run Propensity(LRP)라고 부릅니다.
즉 어떠한 변화가 t-시점 이후로 쭉 유지된다면, 이 정책이 가져오는 영구적인 효과를 측정하는 것이라고 해석할 수 있겠죠.

하지만 이러한 FDL Model의 문제점은 위와 같습니다.
t-시점의 자료와 그 이전 시점의 자료 간의 AutoCorrelation이 존재하는 경우가 많습니다.
그렇기에 이러한 상관성이 높은 자료들을 설명변수로 사용할 경우 다중공선성 문제가 발생할 수 있죠.
그러므로 다중공선성 하에서 제대로 된 회귀계수를 추정할 수 없기 때문에 모형 해석에 큰 어려움이 발생합니다.
다음 포스팅에서는 시계열 자료를 이용한 OLS회귀분석의 몇 가지 Basic한 가정들에 대해서 알아보도록 하겠습니다.
감사합니다.
잘 읽으셨다면 게시글 하단에 ♡(좋아요) 눌러주시면 감사하겠습니다 :)
(구독이면 더욱 좋습니다 ^_^)
- 간토끼(DataLabbit)
- University of Seoul
- Economics, Data Science
'Statistics > Econometrics' 카테고리의 다른 글
| [계량경제학] 시계열 회귀분석의 고전적 가정(2) (0) | 2021.04.11 |
|---|---|
| [계량경제학] 시계열 회귀분석의 고전적 가정(1) (1) | 2021.04.10 |
| [계량경제학] 시계열 회귀분석(Time Series Regression)의 개념 (0) | 2020.12.18 |
| [계량경제학] Measurement Error in the Independent Variable (0) | 2020.12.14 |
| [계량경제학] Measurement Error in the Dependent Variable (0) | 2020.11.03 |
