Review
참고 포스팅 :
2020/11/03 - [Statistics/Econometrics] - [계량경제학] Measurement Error in the Dependent Variable
[계량경제학] Measurement Error in the Dependent Variable
안녕하십니까, 간토끼입니다. 이번 포스팅은 사회과학 연구 중 빈번하게 발생하는 Measurement Error(측정오차)에 대해서 다뤄보겠습니다. 총 2부의 포스팅으로 나누어 작성할 계획이며, 첫 번째는
datalabbit.tistory.com
안녕하십니까, 간토끼입니다.
지난 포스팅에서는 반응변수 Y에 Measurement Error가 발생하는 case에 대해 다뤄보았다면,
이번 포스팅은 설명변수 X에 Measurement Error가 발생하는 case에 대해 다뤄보겠습니다.

잠시 지난 포스팅을 review해보도록 하죠.
반응변수 y에 Measurement Error가 발생하는 경우는 사실 2가지 가정만 만족하면 큰 문제는 되지 않았습니다.
먼저 Measurement error를 e라고 정의하면,
(1) E(e) = 0 : 측정오차 e의 기댓값은 0이다.
(2) 측정오차 e는 random => 측정오차 e와 설명변수 X 간 상관관계는 없다.
이 2가지 가정만 만족하면 OLS 추정량은 불편성, 일치성을 만족한다고 했었죠.
그리고 이러한 가정들이 크게 만족하기 어려운 가정은 아닐 것으로 판단됩니다.
그러나 설명변수에 Measurement Error가 발생하는 경우는 조금 더 따져봐야 할 문제가 있습니다.
한번 살펴보도록 하죠.

먼저 쉽게 접근하기 위해 설명변수가 1개만 존재하는 simple regression을 예로 들어보겠습니다.
이때 위 모델은 Gauss-Markov Assumptions을 만족한다고 가정해보죠.
그러므로 위 모델의 OLS 추정량은 BLUE일 것입니다.
그러나 참값 X* 대신 Measurement Error가 존재하는 X를 모델에 넣고 사용한다면 어떻게 될까요?

지난번과 동일하게 측정오차를 위와 같이 잘못 측정된 x에서 참값 x*를 빼준 값으로 정의할 수 있습니다.
그렇다면 Measurement Error가 포함된 식은 위와 같이 쓸 수 있겠죠.
우선 모형의 오차항이 기존 오차항 u에 βe만큼 빼준 값으로 바뀐 것을 확인하실 수 있으실 겁니다.
이때 마찬가지로 Measurement Error에 대한 몇 가지 가정을 해보죠.

첫 번째 가정은 잘못 측정된 변수 X와 Measurement Error 간 Covariance는 0이라는 가정이고,
두 번째 가정은 참값 X*와 Measurement Error 간 Covariance는 0이 아니라는 가정입니다.
만약 이러한 가정이 모두 만족된다면 OLS추정량은 불편성과 일치성을 만족합니다.
그리고 2번째 가정이 0이 아니라고 했는데요.
구체적으로 구해보면 Measurement Error의 분산의 마이너스값만큼 Covariance가 존재함을 알 수 있습니다.
우리는 Measurement Error가 존재할 때 새로운 오차항을 u-βe 라고 정의하였습니다.
이 새로운 오차항에 대하여 좀 더 살펴보도록 하죠.

먼저 u-βe의 기댓값은 0이 됩니다. u의 기댓값은 당연히 0이고, Measurement Error의 기댓값도 0이라는 가정을 했죠.
그리고 u-βe와 설명변수 간 Covariance는 0이 됩니다.
오차항 u와 0이 되는 건 아실 거고, 위에서 Measurement Error e와 잘못 측정된 X 간 Covariance가 0이 된다고 가정을 했었기 때문이죠.
마지막으로 새로운 오차항의 분산은 기존 오차항의 분산에 β^2 x e의 분산 만큼 더해지는 것을 알 수 있습니다.
수식 없이 자판으로 치려니 참 힘드네요...
이제 여기서 중요한 얘기를 한번 해보죠.
만약 위에서 가정한 "2번째 가정 : 참값 X*와 Measurement Error 간 Covariance는 0이 아니다." 가정이 깨지면 어떻게 될까요?
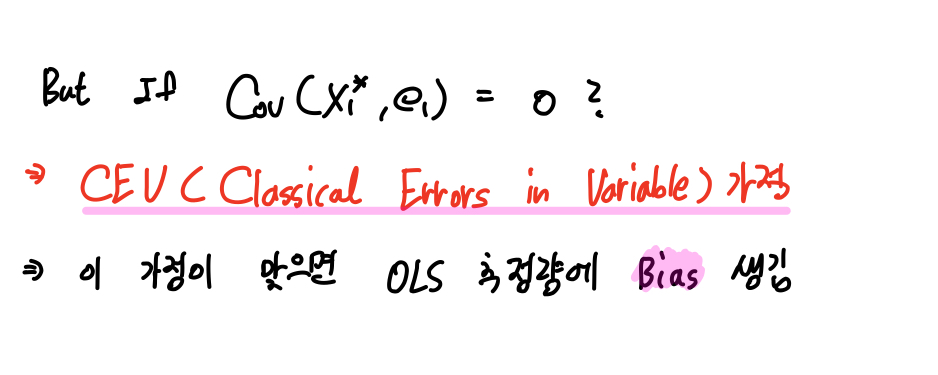
즉 참값 X*와 e 간 Covariance가 0이 되는 거죠.
이를 CEV(Classical Errors in Variable) 가정이라고 합니다.
만약 이 가정이 성립하면 OLS추정량에 Bias가 생겨, 더이상 불편성, 일치성을 만족할 수 없게 됩니다.
왜 그럴까요?

계속 하고 있는 가정을 한번 살펴보죠.
기존 오차항 u와 설명변수 간 상관관계가 0이라는 것은 알고 계실 거고요.
만약 CEV 가정이 성립한다면, 우리가 앞서 세웠던 첫 번째 가정 Cov(X, e) = 0 이 위와 같이 깨지게 됩니다.

그렇기에 잘못 측정된 설명변수 X와 새로운 오차항 간 Covariane가 0이 아니게 되는 문제가 발생합니다.
이는 "오차항과 설명변수 간 상관관계는 없다"라는 회귀모형의 가정을 위배하게 됩니다.
즉 모형의 내생성 문제가 발생하게 되죠. 이는 필연적으로 OLS추정량에 Bias를 일으킵니다.
다시 한번 살펴보죠.

만약 CEV 가정이 성립하지 않는다면 위와 같이 모형의 내생성 문제는 발생하지 않습니다.
그러나 CEV 가정이 성립한다면 설명변수와 새로운 오차항 간 상관관계가 존재하기 때문에 OLS추정량은 더이상 불편추정량, 일치추정량이 되지 못합니다.
그렇다면 CEV가정 하에서 OLS추정량은 얼마나 일치성(Consistency)을 만족하지 못할까요?

OLS추정량의 확률극한에 따라 식을 전개해보면 위와 같습니다.
즉 OLS추정량에 1보다 작은 값을 곱하는 꼴로 표현이 되는데요.
이렇게 1보다 작은 값을 곱함으로써 parameter보다 작아지게 되는 bias를 Attenuation Bias라고 합니다.

물론 이러한 Attenuation Bias는 CEV 가정 때문에 생기는 Bias라는 것이죠.
지금까지의 내용을 정리하면 다음과 같습니다.

먼저 설명변수 X에 Measurement Error가 존재할 경우,
만약 이 측정오차와 측정오차가 존재하는 X 간 상관관계가 없다면 큰 문제가 되지 않습니다.
하지만 CEV 가정, 즉 측정오차와 참값 X 간 상관관계가 없다면 이는 큰 문제가 됩니다.
따라서 설명변수에 Measurement Error가 존재해도 CEV가정을 만족하는지, 그렇지 않은지만 파악해보시면 됩니다.
다음 포스팅부터는 Time Series Regression에 대해서 다뤄보도록 하겠습니다.
감사합니다.
잘 읽으셨다면 게시글 하단에 ♡(좋아요) 눌러주시면 감사하겠습니다 :)
(구독이면 더욱 좋습니다 ^_^)
- 간토끼(DataLabbit)
- University of Seoul
- Economics, Data Science
'Statistics > Econometrics' 카테고리의 다른 글
| [계량경제학] Finite Distributed Lag Model(FDL Model) (0) | 2020.12.21 |
|---|---|
| [계량경제학] 시계열 회귀분석(Time Series Regression)의 개념 (0) | 2020.12.18 |
| [계량경제학] Measurement Error in the Dependent Variable (0) | 2020.11.03 |
| [계량경제학] Proxy Variable(대리변수) (0) | 2020.10.26 |
| [계량경제학] Test Against Nonnested Alternatives (4) | 2020.10.24 |
