안녕하십니까, 간토끼입니다.
이번 포스팅은 사회과학 연구 중 빈번하게 발생하는 Measurement Error(측정오차)에 대해서 다뤄보겠습니다.
총 2부의 포스팅으로 나누어 작성할 계획이며, 첫 번째는 반응변수 y에 Measurement Error가 발생하는 case에 대해서 다뤄보겠습니다.

1. Measurement Errror(측정오차)
측정오차의 정의는 다음과 같습니다.

흔히 사회과학에서 survey를 하다 보면 발생하는 경우라고 할 수 있는데요.
설문조사 시 응답자가 아무래도 자신의 기억을 더듬어가며 응답하다보니, 잘못 응답하는 실수가 발생할 수 있습니다.
예를 들어 개인의 연봉에 대해서 조사할 때, 실제로는 5282만원이지만, 그냥 5200만원으로 응답한다든지,
혹은 일별 TV시청시간에 대해서 물을 때 실제로는 3시간 52분을 시청했으나 대충 3시간 정도 봤다고 응답한다든지...
이러한 오차가 크지 않다면 심각한 문제는 아닐 수 있으나, 만약 오차에 어떠한 패턴이 있다든가, 혹은 오차가 생각보다 큰 경우를 생각해보면 잘못된 데이터를 이용해 모집단을 일반화한다면 잘못된 추론 결과를 가질 수도 있죠.
우리는 계량경제학에서의 문제를 따지고 있으므로, Regression Model에서 이러한 정확하지 않은 측정값이 존재할 때 어떻게 해결하면 좋을지 살펴보도록 하겠습니다.
먼저 y 변수, 즉 반응변수에 Measurement Error가 발생할 때 Regression Model에서 어떤 점을 주의하면 좋을지 따져보도록 하죠.
아 그냥 말씀드리자면 보통은 종속변수라는 용어를 많이 쓰지만, 저는 '반응변수'라는 용어를 사용해 Y 변수를 가리킵니다.
큰 차이는 없는데, 아무래도 회귀분석이 인과관계가 아닌 상관관계를 기반으로 변수 간 관계를 정의하므로, 종속변수라는 용어를 사용하면 인과적인 측면을 좀 더 부각하는 느낌이 있어서요.
잘못된 인식(?)까진 아니지만 부정확한 인식을 줄 수 있다는 생각에 개인적으로 설명변수, 반응변수란 용어를 좋아합니다.
그래서 개인적으로 독립변수 대신 설명변수를, 종속변수 대신 반응변수라는 용어를 사용하니 착오 없으시길 바랍니다.
각설하고 한번 살펴보도록 하죠!

먼저 다음과 같이 y*를 참값, 그리고 y를 잘못 측정된 값, 즉 Measurement Error 가 존재하는 값으로 정의하겠습니다.
Error가 없다면 둘이 같겠지만, 우리는 Error가 있는 경우를 따지고 있으므로 통상적으로 둘은 같지 않은 값이겠죠.
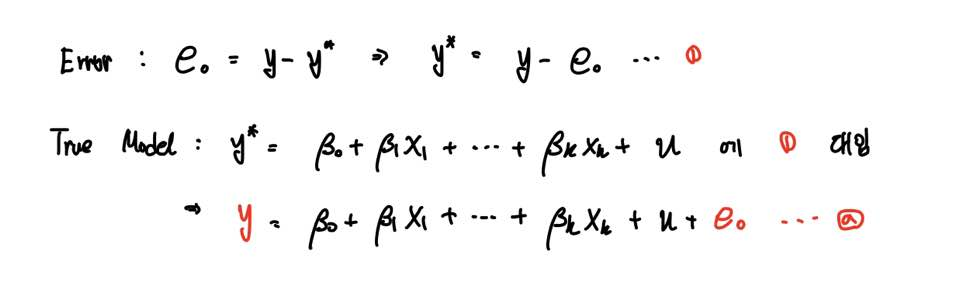
그렇기에 Measurement Error를 잘못 측정된 y값에서 참값을 빼준 것으로 정의할 수 있습니다.
부호가 정해진 것은 아니므로 y*에서 y를 빼줘도 무방하지만 아래의 식을 편하게 만들기 위해 이렇게 쓴다고 이해하시면 됩니다.
자 그래서 Measurement Error를 반영하면 우변에 error e를 더한 값으로, 좌변은 y로 식(a)와 같이 정의할 수 있습니다.
그리고 위 식은 Gauss-Markov Assumptions을 만족한다고 가정하겠습니다.
그렇다면 우리는 위 Measurement Error에 대해 다음과 같은 가정을 가정하겠습니다.

첫 번째 가정은 Measurement Error의 기댓값은 0이라는 가정이고,
두 번째는 이러한 Error가 랜덤으로, 설명변수 X들과 Uncorrelated 하다는 것이죠.
만약 이러한 가정이 모두 만족된다면 Error가 전혀 문제가 되지 않습니다.
즉 OLS추정량은 이전과 동일하게 불편성과 일치성을 만족합니다.
그러나 1번 가정(Error의 기댓값은 0)을 만족하지 못하면 어떻게 될까요?

즉 Measurement Error의 기댓값이 0이 아닌 임의의 상수라고 가정해보죠.
그렇다면 모형의 Fitted value를 보면 절편 상수항의 값이 β0^ 가 아닌 상수 a를 더한 (β^+a) 가 됩니다.
즉 a 만큼의 Bias가 발생합니다.
하지만 기울기계수가 아닌 상수항에 Bias가 생기는 것은 큰 문제는 아닙니다.
우리가 알고 싶은 것은 변수 간의 관계의 정도를 나타내는 기울기계수니깐요.
또 Usual한 가정인 실제 모형의 오차항인 u와 Measurement Error인 e 간의 Covariance 가 0인 경우를 떠올려보겠습니다.
즉 두 오차항의 공분산이 0이므로, 상관관계가 없다는 의미겠죠.

우리가 y에 Measurement Error가 존재하는 모형을 식(a)라고 정의하였으므로,
이때의 오차항을 v = u + e 라고 정의해보죠.
그렇다면 오차항의 분산 Var(u)는 위 과정에 의해 Measurement Error의 분산만큼 커집니다.
만약 Cov(u, e)가 0이 아니라면 분산은 더 커지게 되겠죠?
그렇다면 결론적으로 OLS추정량의 분산이 다소 커지게 됩니다.

다중회귀분석에서의 추정량의 분산 공식을 떠올려보시면 이해가 되시겠죠.
사실 그렇다고 해도 이것이 큰 문제는 아닙니다.
즉 결론적으로 반응변수 Y에 Measurement Error가 존재하여도 큰 문제는 되지 않습니다.
위 가정을 만족한다면 그냥 OLS하면 됩니다.
다만 설명변수 X에 Error가 존재하는 경우는 조금 얘기가 달라집니다.
다음 포스팅에서 다뤄보도록 하죠.
감사합니다.
잘 읽으셨다면 게시글 하단에 ♡(좋아요) 눌러주시면 감사하겠습니다 :)
(구독이면 더욱 좋습니다 ^_^)
- 간토끼(DataLabbit)
- University of Seoul
- Economics, Data Science
'Statistics > Econometrics' 카테고리의 다른 글
| [계량경제학] 시계열 회귀분석(Time Series Regression)의 개념 (0) | 2020.12.18 |
|---|---|
| [계량경제학] Measurement Error in the Independent Variable (0) | 2020.12.14 |
| [계량경제학] Proxy Variable(대리변수) (0) | 2020.10.26 |
| [계량경제학] Test Against Nonnested Alternatives (4) | 2020.10.24 |
| [계량경제학] Ramsey RESET test (0) | 2020.10.24 |
