Review
참고 포스팅 :
2020/11/03 - [Statistics/Time Series Analysis] - [시계열분석] 시계열모형의 개념
[시계열분석] 시계열모형의 개념
안녕하십니까, 간토끼입니다. 이번 포스팅은 시계열분석의 첫 포스팅인 시계열모형의 개념에 대해서 소개해보겠습니다. 우리가 일반적으로 시계열자료(Time Series)라고 부르는 것들은 주변에서
datalabbit.tistory.com
안녕하십니까, 간토끼입니다.
지난 포스팅에서는 시계열모형이 무엇인지에 대한 개념을 다루었습니다.통상적으로 시계열분석이라고 하면 시계열자료를 이용한 예측(Forecasting)에 대해서 많이 다루는데요.
이번 포스팅부터는 시계열자료를 이용한 예측 기법에 대해서 하나씩 다뤄보겠습니다.
그러한 의미에서 이번 포스팅은 시계열자료의 추세(trend)를 이용한 추세분석인 다항추세모형 중 상수평균모형에 대해서 다뤄보겠습니다.

1. 추세모형이란?
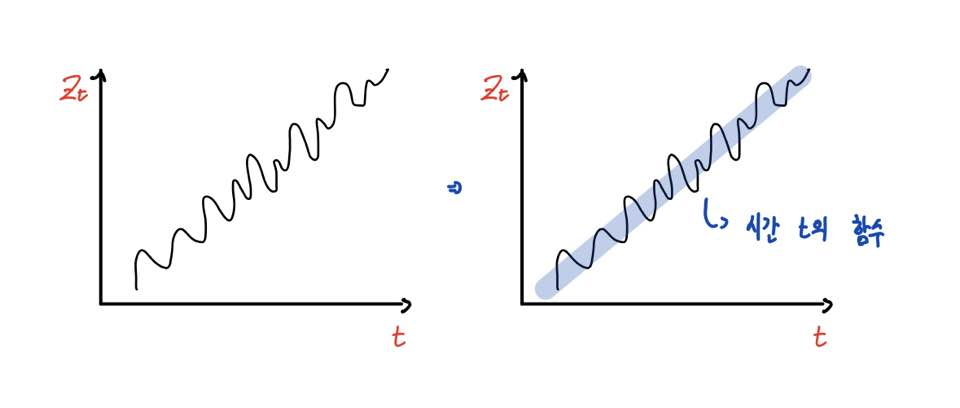
다음과 같이 가로축(x축)을 시간 t, 그리고 세로축(y축)을 자료 Z로 놓고 시계열그림을 살펴보도록 하죠.
지난 포스팅에서도 추세성분에 대해서 다루면서 이 얘기를 했었지만,
우리가 보고자하는 자료가 시간에 따라 증가 혹은 감소하는 어떠한 추세를 보인다면 이는 시간 t에 대한 함수로 나타낼 수 있습니다.
만약 이렇게 추세가 보이는 자료들을 이용해 OLS 회귀분석을 한다고 하면 이 경우는 크게 문제가 됩니다.
왜냐하면 추세가 존재하는 자료끼리 회귀분석을 할 경우, 아무런 노력을 들이지 않고도 단순히 추세로 인해 유의한 상관관계가 존재한다고 판별할 수 있기 때문에, 잘못된 결론을 내리게 되는 spurious regression problem 가 발생합니다. (추후 계량경제학 카테고리에서 다룰 예정입니다.)
그러나 추세를 이용해 값을 예측(Forecasting)할 목적이라면, 이러한 추세를 적절히 이용하는 것이 중요합니다.
그러한 의미에서 추세모형은 다음과 같이 나타낼 수 있습니다.

관측값 Z를 위와 같이 시간 t에 대한 Polynomial term을 이용하여 다항식으로 나타낼 수 있습니다.
이를 선형다항추세모형(Linear Polynomial Trend Model), 혹은 편하게 다항추세모형이라고 합니다.

이러한 다항추세모형은 사실 설명변수가 시간 t의 함수인 다중회귀모형(Multiple Linear Regression Model)의 특별한 case입니다.
설명변수인 Trend를 이용해 반응변수 Z를 예측하는 개념이니깐요.
그렇다면 이러한 다항추세모형 중 가장 쉬운(?) 모형인 상수평균모형에 대해서 다뤄보도록 하죠.
2. 불규칙 성분만을 갖는 경우 : 상수평균모형
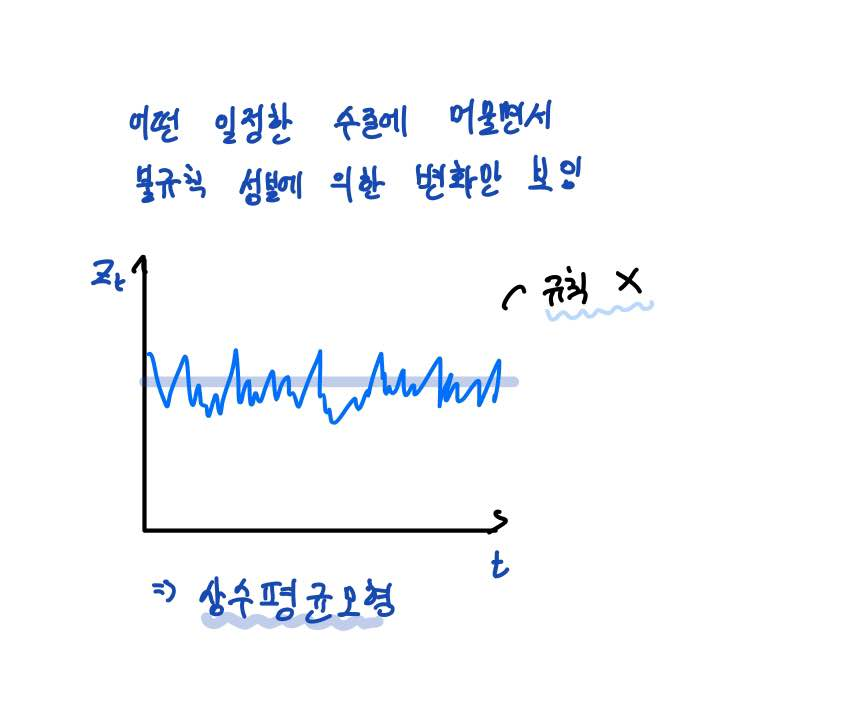
상수평균모형의 설명을 위해 위 그림을 한번 살펴보겠습니다.
이전 포스팅에서 시계열그림의 유형을 다루면서 살펴봤던 시계열그림인데요.
우리가 다루고자 하는 자료 Z가 위와 같이 일정한 수준에 머물면서 불규칙 성분에 의한 변화만을 보일 경우,위 자료는 상수평균모형으로 설명이 가능합니다.

상수평균모형은 자료가 일정한 수준(상수)에 머물면서 불규칙 성분(오차항)에 의한 변화만을 보일 때 설명한다고 했죠?
일정한 수준에 머문다는 얘기는 임의의 상수를 의미하고, 불규칙 성분은 지난 포스팅에서 회귀모형의 오차항에 해당한다고 정의했습니다.
그러므로 오차항은 Cross-sectional data를 이용한 회귀분석에서의 오차항에 대한 가정인 i.i.d를 따르겠죠.어떠한 패턴 없이 불규칙하게 움직여야 하니깐요.

그래서 먼저 이러한 상수평균모형의 모수(Parameter)는 β가 되며, 이 β의 LSE는 β^ = 자료 Z의 평균 이 됩니다.
우리가 미래의 자료를 예측한다고 하면 가장 무난하고 안전한 방법은 현재까지의 데이터의 평균 혹은 기댓값을 사용하잖아요?
왜냐하면 자료의 기댓값을 사용하면 예측값의 오차를 작게 하는 효과적인 방법이기 때문이죠.
괜히 평균 키가 170cm인 집단에서 신입 회원의 키를 예측할 때 182cm! 라고 하면 맞을 수도 있겠지만 그렇지 않을 확률이 더 크겠죠.
하지만 170cm라고 답할 경우, 실제로는 173cm라 해도 오차가 182cm라고 했을 때의 경우보다는 작아지니까 그나마 안전한 선택이 되는 거죠.
그러므로 현 시점에서 가장 바람직한 l-시차 후의 예측값은 β^ 이 됩니다.
왜냐하면 상수평균모형은 시계열자료가 일정한 수준에 머무는 trend를 보일 때 적용하는 모형이라고 했으니깐요.
미래에도 현재의 trend에서 크게 벗어나지 않을 것이란 게 바람직한 가정이겠죠?

그러므로 l-시차 후의 예측값의 오차인 예측오차 e^ 은 위와 같이 정의할 수 있습니다.
따라서 이 예측오차의 기댓값은 0이 됩니다.왜냐하면 Z의 평균은 β^이고, β^의 기댓값은 β가 되기 때문이죠.
분산 또한 위와 같은 과정으로 구해주면 됩니다.어렵지 않으실 거라 생각합니다.
참고로 시계열분석은 회귀분석을 선수 지식으로 요구합니다.
따라서 시계열분석에 관심있으신 분들은 최소한 회귀분석 포스팅은 한번 정도 읽고와주시면 좋을 것 같습니다.
감사합니다.
잘 읽으셨다면 게시글 하단에 ♡(좋아요) 눌러주시면 감사하겠습니다 :)
(구독이면 더욱 좋습니다 ^_^)
- 간토끼(DataLabbit)
- 학부 4학년(a fourth-grade undergraduate)
- University of Seoul
- Economics, Data Science
'Statistics > Time Series Analysis' 카테고리의 다른 글
| [시계열분석] 단순지수평활법(Simple Exponential Smoothing Method) (0) | 2020.11.16 |
|---|---|
| [시계열분석] 자기회귀오차모형(Autoregressive Error Model) (2) | 2020.11.12 |
| [시계열분석] Durbin-Watson(DW) Test (4) | 2020.11.11 |
| [시계열분석] 다항추세모형(2) - 선형추세모형(Linear Trend Model) (5) | 2020.11.06 |
| [시계열분석] 시계열모형의 개념 (4) | 2020.11.03 |
