안녕하십니까, 간토끼입니다.
이번 포스팅은 시계열분석의 첫 포스팅인 시계열모형의 개념에 대해서 소개해보겠습니다.

우리가 일반적으로 시계열자료(Time Series)라고 부르는 것들은 주변에서 흔히 볼 수 있는 것들입니다.
가장 무난하게는 여러 경제지표들이 있겠죠. (GDP, 소비자물가지수, 실업률 등)
혹은 연별 범죄 발생 건수, 일별 강우량 등 데이터를 예로 들 수 있겠습니다.
이들의 공통점은 "시간"을 기준으로 데이터가 관측된다는 것입니다.
1분 단위로 측정될 수도 있고, 시간 단위로 측정될 수도 있으며, 일별 단위로 측정될 수 있겠죠.
거시적인 지표일수록 측정 주기가 길어질 것이고요.

이처럼 시계열자료는 횡단면자료에서 관측치를 i를 기준으로 측정한 것과 다르게,
시간 t를 기준으로 측정하는 자료입니다.
그러므로 변수의 하첨자가 i가 아닌 t를 사용하게 됩니다.
당연하게도 t가 작아질수록 시간이 멀어지는 것이고요.

그래서 핵심은 이러한 시계열자료는 관측 주기가 동일해야 합니다.
이를 시차(Time lag)이라고 하는데요.
즉 일별 자료라면, 자료 간의 간격인 시차가 1일로 동일해야 한다는 것입니다.
만약 일별 자료임에도 불구하고 간격이 1일, 3일, 2일 3시간, 5일 10시간 .... 이렇게 된다면 올바른 추정을 할 수 없게 되겠죠?
위에서 언급한 바와 같이 시계열자료는 시간의 영향을 받습니다.
주가(Stock Price)를 예로 들면, 오늘의 주가는 일주일 전의 주가보다 어제의 주가에 영향을 받습니다.
예를 들어 어제 2000이었다면, 오늘은 2000에 근접한 값에 위치할 것이라고 '일반적으로' 예상할 수 있겠죠.
만약 2일전 : 1900원, 1일전 : 2000원 이라면 오늘은 2000원보다 커질 것이라는 추세(Trend)도 예상해볼 수 있겠고요.
그러므로 횡단면 자료에서 i.i.d(identically independent distribution) 가정을 했던 것과 다르게 independent 가정을 적용하기 다소 어려워 보입니다.
즉 자료 간 독립이 아니게 되어 상관성이 존재한다는 것이죠.
따라서 이러한 자료들 간 상관성을 바탕으로 이에 맞는 분석법이 필요합니다.
뭐 이러한 건 추후 다뤄보도록 하고요.

시계열은 크게 위와 같은 성분으로 구성되어있다고 봅니다.
불규칙성분, 추세성분, 계절 혹은 순환성분으로 이루어져 있는데요.
하나씩 한번 살펴보시죠.
1. 불규칙성분
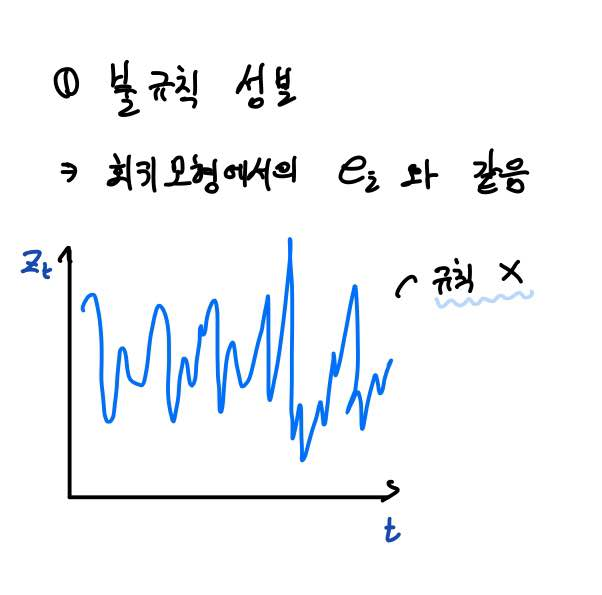
불규칙성분은 회귀모형에서의 오차항(Error term)과 같습니다.
즉 시간에 따라 규칙적인 움직임과 무관하게 랜덤한 원인에 의해 나타나는 변동성분을 의미합니다.
그러므로 우리가 특정한 규칙이 없어 뭐랄까 특별히 설명할 수 없는 성분이죠. 오차항이라고 간주하셔도 됩니다.
2. 추세성분
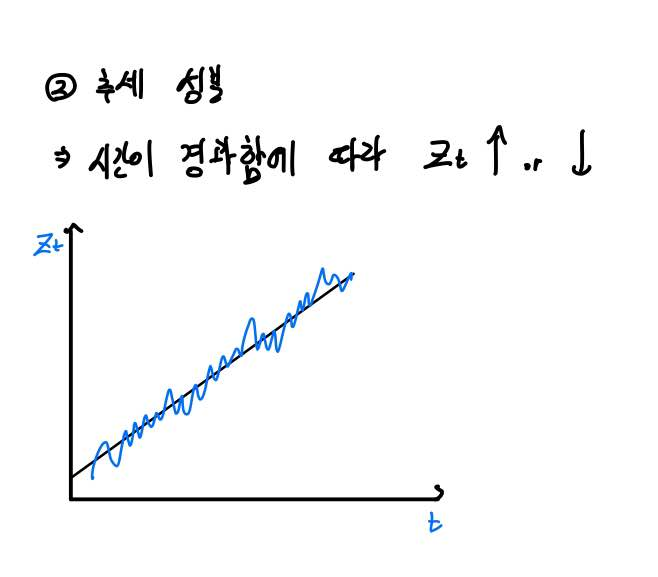
추세성분은 불규칙성분과는 달리 시간이 경과함에 따라 관측값이 지속적으로 증가하거나 감소하는 추세를 갖는 경우의 변동을 의미합니다.
위 그림은 선형추세(Linear Trend)를 나타내고 있는데요.
이러한 추세가 반드시 직선일 필요는 없고, 2차 곡선이나 3차 곡선의 형태로도 나타날 수 있습니다.
특히 거시경제의 여러 자료를 보면 시간이 흐름에 따라 상승하는 추세를 보이는데요.
예를 들어 소비지출과 같은 자료는 하방경직적이라고 하죠.
한번 상승하고 나면 잘 하락하지 않는 것을 의미합니다.
이러한 경우, 다음 시점의 값을 예측(Prediction)할 때, 이러한 추세(trend)를 고려해주는 것이 좋겠죠?
3. 계절성분(or 순환성분)
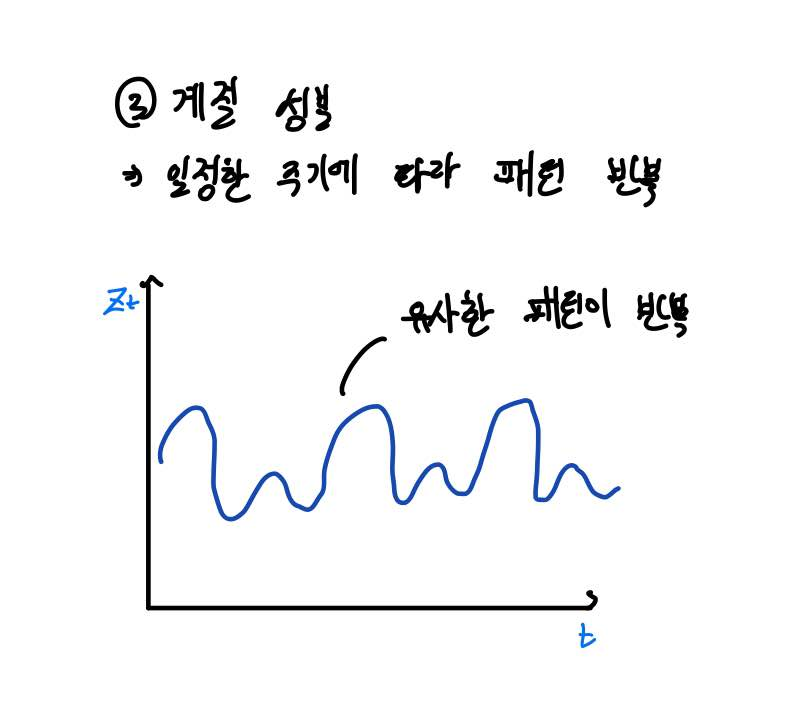
계절성분은 말 그대로 계절과 같은 일정한 주기에 따라 유사한 패턴이 반복되는 것을 말합니다.
그림이 좀 발그림이긴 하지만... 위와 같이 시간이 흐름에 따라 유사한 패턴이 계속 반복되는 거죠.
예를 들어 연말 크리스마스 시즌, 혹은 추석이나 설날 등 명절에 선물을 사려는 수요가 다른 시기에 비해 굉장히 많죠?
그렇다면 월별 백화점 매출액 자료를 살펴보면, 추석 / 연말(크리스마스) / 연초(설날) 시즌엔 다른 시기와 달리 매출액 데이터가 클 것이며, 이는 매년 유사한 패턴을 보이며 반복할 것입니다.
이런 경우 계절성분, 혹은 순환성분이 존재한다고 합니다.
그렇다면 이러한 성분이 한꺼번에 나타날 수도 있겠죠?

다음과 같이 추세성분과 계절성분이 동시에 나타나는 경우도 쉽게 떠올려볼 수 있겠죠.
백화점의 경우, 잘 나가는 곳이라면 매년 매출액은 점차적으로 증가할 것이고요.
그리고 추석 / 연말(크리스마스) / 연초(설날) 시즌엔 다른 시기와 달리 매출액 데이터가 크다고 하면 위와 같은 형태를 보일 것입니다.
그렇다면 위 경우에서 백화점의 잘 나가는 정도(?)가 매년 점점 커진다면 어떻게 될까요?
즉 증가폭이 점점 커지는 경우, 이분산성(heteroskedasticity)이 존재한다는 것이죠.

그렇다면 위와 같은 모습을 보일 것입니다.
이럴 때 이분산성의 감소를 위해 Log Transformation을 취해주면 이분산의 크기를 감소시켜줄 수 있습니다.
위와 같이 시간 t를 x축으로, 시계열 관측값 Zt를 y축으로 하여 그리는 그림을 시계열그림(Time Series Plot)이라고 하며,
우리가 다루고자 하는 시계열에 위 성분들이 존재하는지 직관적으로 파악할 수 있기 때문에 꼭 시계열그림을 그려보는 것이 중요합니다.
다음 포스팅은 시계열분석의 방법론인 추세분석부터 다뤄보겠습니다.
감사합니다.
잘 읽으셨다면 게시글 하단에 ♡(좋아요) 눌러주시면 감사하겠습니다 :)
(구독이면 더욱 좋습니다 ^_^)
- 간토끼(DataLabbit)
- 학부 4학년(a fourth-grade undergraduate)
- University of Seoul
- Economics, Data Science
'Statistics > Time Series Analysis' 카테고리의 다른 글
| [시계열분석] 단순지수평활법(Simple Exponential Smoothing Method) (0) | 2020.11.16 |
|---|---|
| [시계열분석] 자기회귀오차모형(Autoregressive Error Model) (2) | 2020.11.12 |
| [시계열분석] Durbin-Watson(DW) Test (4) | 2020.11.11 |
| [시계열분석] 다항추세모형(2) - 선형추세모형(Linear Trend Model) (5) | 2020.11.06 |
| [시계열분석] 다항추세모형(1) - 상수평균모형 (0) | 2020.11.04 |
