Review
참고 포스팅 :
2020/10/10 - [Statistics/Regression Analysis] - [회귀분석] 최소제곱추정량 β1를 선형 추정량으로 유도하기
안녕하십니까, 간토끼입니다.
이번 포스팅에서는 회귀모형의 조금 특수한 형태인 원점을 지나는 회귀모형(Regression Through the Origin)에 대해 다뤄보도록 하겠습니다.

어려운 개념은 아닙니다.
원점을 지난다는 얘기는 다른 말로 하면 회귀모형의 상수항(절편)인 β0 = 0이라는 것이므로,
단순회귀분석 문제 하에서 우리가 추정하는 Parameter는 기울기 계수인 β 하나밖에 없습니다.
중학교 때 배웠던 y 절편이 없는 일차함수 꼴을 떠올려보면 금방 이해하실 겁니다.

즉 추정할 Parameter의 개수가 줄어들었으므로, 문제가 좀 더 단순하겠죠?
그래서 오늘 다룰 내용도 이전 내용을 충분히 이해하셨다면 전혀 무리없이 이해할 수 있을 거라 생각합니다.
원점을 지나는 회귀모형 문제는 뭐랄까 회귀분석 시험에서 심심치 않게 출제되는 것으로 알고 있습니다.
저같은 경우도 저희 학교 수업의 이전 기출을 풀다가 만난 적도 있었고, 실제 회귀분석및실습 중간고사 문제에서도 나왔었던 것으로 기억합니다.
(과제였는지 시험이었는지... 아마 시험이었던 것 같은데...)
막 어렵고 중요한 개념은 아니라 수업에서는 크게 안 다루시는데,
시험에서는 종종 내시더라고요.
물론 단순회귀분석의 개념을 다 이해하셨으면 무리없이 시험에서 처음 만나도 푸실 수 있으나,
사람 일이란 게 혹~시 모르니, 당황하시기 전에 살펴보고 가시면 좋습니다.
각설하고 한번 다뤄보죠.
1. β의 최소제곱추정량(LSE of β) 구하기

우리가 이전 포스팅 중 최소제곱법을 이용해 최소제곱추정량을 이용했던 포스팅에서 추정량을 직접 유도해보았는데요.(게시글 상단에 링크 있습니다.)
마찬가지로 최소제곱법(Least Square Method)을 이용해 최소제곱추정량을 유도해줍니다.
다만 Parameter가 하나밖에 없어 식이 매우 간단합니다.
쉽게 보일 수 있죠?
2. 추정량 β^을 선형추정량(Linear Estimator)으로 유도

마찬가지로 일반적인 단순회귀모형에서 다루었던 방식 그대로 추정량을 선형추정량 형태로 유도합니다.
이렇게 하는 이유는 계산을 쉽게 하기 위한 목적이 아니라, 추정량의 이론적 특성을 검토하고 기댓값과 분산을 쉽게 유도하기 위함이라고 했죠.
추정량 β^ 또한 모수(Parameter)에 오차항에 대한 식 ∑kiei 을 더해준 꼴로 나타낼 수 있으며,
마찬가지로 ∑kixi = 1라는 성질을 이용하였습니다.
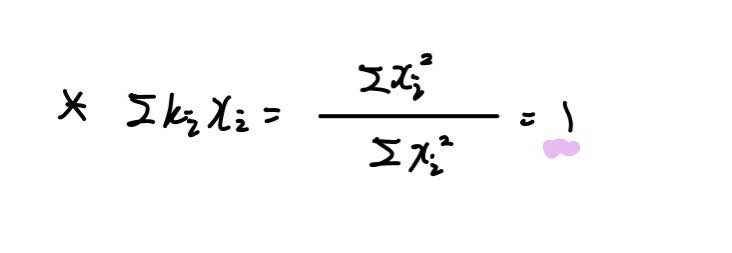
이는 가볍게 보일 수 있죠.
이전 포스팅을 읽어보셨던 분들이라면 이정도는 굳이 설명 안해도 상관없을 것 같습니다.
그래서 이러한 선형추정량을 바탕으로 기댓값과 분산을 유도해보겠습니다.
3. 추정량 β^의 기댓값 구하고 불편성 보이기

사실 추정량의 불편성을 보이는 문제는 이제 너무나 쉽습니다
바로 분산으로 넘어가보죠.
4. 추정량 β^의 분산 구하기

분산도 식이 생각보다 간단하여, 쉽게 보일 수 있습니다.
∑k^2 에 대한 부분만 짚고 넘어가보죠.

이를 통해 ∑k^2 를 보일 수 있습니다.
아마 계량경제학, 혹은 회귀분석 수업 등을 들으시는 분들은 이러한 유사한 문제들이 많이 나옵니다.
모형을 조금 특수하게 설정하여 y = a + ei 등 상수항만 존재하는 모형, 혹은 추정량을 잘못 계산한 모형의 불편성을 보이는 등 여러 케이스가 있는데요.
처음 보면 당황하실 수도 있지만, 제가 포스팅에서 계속 강조하며 다루고 있는 맥락을 잘 파악하시면,
그러한 유형이 나와도 쉽게 접근할 수 있으실 겁니다.
추정량? 오케이 선형추정량으로 유도해 -> 불편성 보여, 보였어? 그럼 분산 유도해!
약간 이런 맥락으로 ㅎㅎ
아무튼 요즘 시험기간이라 블로그 인기가 좀 많은데요.
혹~시나 보시다가 궁금한 점, 혹은 알고 싶은 부분이 있으시면 댓글 남겨주세요.
감사합니다.
잘 읽으셨다면 게시글 하단에 ♡(좋아요) 눌러주시면 감사하겠습니다 :)
(구독이면 더욱 좋습니다 ^_^)
- 간토끼(DataLabbit)
- University of Seoul
- Economics, Big Data Analytics
'Statistics > Regression Analysis' 카테고리의 다른 글
| [회귀분석] 유의수준과 유의확률 (4) | 2022.03.03 |
|---|---|
| [회귀분석] 가설검정의 기초 개념 (0) | 2022.03.03 |
| [회귀분석] 최소제곱추정량 β0의 기댓값, 분산 유도 (12) | 2020.10.20 |
| [회귀분석] 가우스-마르코프 정리(Gauss-Markov Theorem) 증명 (16) | 2020.10.14 |
| [회귀분석] 최소제곱추정량 β1의 기댓값, 분산 유도 (5) | 2020.10.13 |
