Review
참고 포스팅 :
2020.05.21 - [Statistics/Basic Statistics] - [기초통계학] 확률(Probability) 2 - 결합확률, 주변확률, 조건부확률
[기초통계학] 확률(Probability) 2 - 결합확률, 주변확률, 조건부확률
Review 참고 포스팅 : 2020/05/20 - [Statistics/Basic Statistics] - [기초통계학] 확률(Probability) 1 - 확률의 기본 개념 [기초통계학] 확률(Probability) 1 - 확률의 기본 개념 Review 참고 포스팅 : 2020/05/18 - [Statistics/Ba
datalabbit.tistory.com
2020.05.25 - [Statistics/Basic Statistics] - [기초통계학] 확률(Probability) 3 - 베이즈 정리(Bayes’ theorem)
[기초통계학] 확률(Probability) 3 - 베이즈 정리(Bayes’ theorem)
Review 참고 포스팅 : 2020/05/20 - [Statistics/Basic Statistics] - [기초통계학] 확률(Probability) 1 - 확률의 기본 개념 [기초통계학] 확률(Probability) 1 - 확률의 기본 개념 Review 참고 포스팅 : 2020/05/18 - [Statistics/Ba
datalabbit.tistory.com
# 해당 포스팅은 KOCW 김충락 교수님의 수리통계학 강의와 Hogg의 수리통계학개론(Introduction to Mathematical Statistics)를 기초로 작성되었습니다.
안녕하십니까, 간토끼입니다.
이번 포스팅에서는 조건부 확률과 베이즈 정리(Conditional Probability and Bayes Theorem)에 대해 다뤄보겠습니다.
사실 이 개념들은 기초통계학 카테고리에서 다뤘었는데요.
수리통계학에서 다시 다루는 만큼, 중복되는 내용보다는 좀 더 수리적인 표현을 사용하여 개념을 설명해보겠습니다.
보다 쉬운 설명을 원하는 분들은 위 참고 포스팅을 참고해주세요.

조건부 확률(Contional Probability)이란 어떤 개념일까요?
이름에서 쉽게 유추할 수 있듯이, 확률에 조건(Condition)이 붙습니다.

즉 조건이 붙는다는 것은 상황을 구체적으로 만들어준다고도 이해할 수 있겠죠.
같은 밥을 먹었냐는 질문에도 '밥 먹었어?'보다는 '제육볶음과 순두부찌개가 차려진 맛있는 밥 먹었어?'가 더 구체적이니까요. (먹고 싶네요 ... )

위와 같은 상황을 생각해봅시다.
고객이 A라는 제품을 구매하는 사건을 A라고 했을 때, 별 다른 언급이 없다면 사건 A는 Sample Space $C$ 의 부분집합이겠죠.
즉 확률 $P(A)$ 는 이 Sample Space로부터 유도된 'A 제품을 구매할 확률' 그 이상도, 이하도 아닐 겁니다.
이때 "B 제품"을 구매한 고객이 A 제품을 구매하는 사건 이라고 조건을 붙여 구체화를 한다면,
이때의 조건 덕분에 A 제품을 어떻게 판매할지에 대한 전략을 구체적으로 세울 수 있겠죠.
조건부 확률은 이러한 상황을 가능하게 해줍니다.
조건부 확률(Conditional Probability)을 정의해봅시다.

사건 $A, B$가 Sample Space $C$의 부분집합일 때,
B가 주어졌을 때의 사건 A의 조건부 확률은 A와 B의 교집합을 사건 B로 나눠준 것과 같습니다.
$$ P(A|B) = \frac{P(A \cap B)}{P(B)} $$
즉 사건 A의 조건부 확률은 $P(A)$의 Sample Space가 전체 집합 $C$ 이었던 것과 다르게 Sample Space는 사건 B로 한정됩니다.
위 벤다이어그램을 보시면 쉽게 이해하실 수 있으실 겁니다.
조건부 확률도 "확률"이기 때문에, 지난 포스팅에서 다루었던 것처럼 다음 확률의 3가지 공리를 만족해야 합니다.

2023.07.07 - [Statistics/Mathematical Statistics] - [수리통계학] 확률집합함수(Probability Set Function)
[수리통계학] 확률집합함수(Probability Set Function)
Review 참고 포스팅 : 2023.07.04 - [Statistics/Mathematical Statistics] - [수리통계학] 집합 이론과 시그마 필드(Set Theory and Sigma-Field) [수리통계학] 집합 이론과 시그마 필드(Set Theory and Sigma-Field) Review # 해당
datalabbit.tistory.com
Non-negativity, Normality, Countable Additivity는 굳이 설명하지 않아도 지난 포스팅을 읽으셨다면 직관적으로 이해하실 수 있겠죠.
그래서 위 조건부 확률은 다른 말로 "사건 B에 대한 조건부 확률집합함수"라고 표현해도 무방해보입니다.
우리는 조건부 확률의 정의로부터 다음과 같은 결과를 보일 수 있습니다.

A와 B의 Joint Probability는 사건 B의 Marginal Prob.(주변 확률)과 A given B의 조건부 확률의 곱으로 나타낼 수 있습니다.
$$ P(A \cap B) = P(B) \times P(A \, | \,B) $$
이를 확률의 곱셈 법칙(Multiplication Rule of Probability)이라고 합니다.

이는 단순히 사건 A, B처럼 2개의 사건뿐만 아니라 3개의 사건에 대해서도 적용될 수 있습니다.
즉 Marginal Prob.과 각각의 Conditional Prob.의 곱들로 표현할 수 있다는 건데요.
$$ P(A \cap B \cap C) = P[ (A \cap B) \cap C ] = P(A \cap B) P(C \, | A \cap B) = P(A)P(B\,|\,A)P(C | A \cap B) $$
만약 n개의 사건의 Joint Prob. 을 구하고 싶으시다면, 이는 다음과 같이 일반화해서 표현할 수 있습니다.

보시면 패턴이 쉽게 보이실 거라 생각합니다.
만약 우변의 다음 항을 쓴다면 $P(C_4 | C_3 \cap C_2 \cap C_1)$ 라고 할 수 있습니다. 어렵지 않죠?
그러면 우린 이제 통계학에서 중요한 정리 중 하나인 베이즈 정리(Bayes Theorem)를 다룰 수 있습니다.

만약 $k$개의 Events $C_1, C_2, \cdots, C_{k}$ 가 Mutually Exclusive하고 Exhaustive한 Set이고, 각 사건의 확률은 0이 아니라고 가정합시다. 즉 $P(C_{i}) > 0, i = 1, 2, \cdots, k$ 이죠.
그러면 이때의 k개의 Event들은 분할(Partition)을 이루고 있다고 할 수 있겠네요.
지난 포스팅에서 이 용어들을 다뤘었죠?
그러면 우리는 어떤 사건 $A$가 주어졌을 때 j번째 사건 $C_j$가 발생할 조건부 확률 $P(C_j | A)$를 다음과 같이 구할 수 있습니다.
$$ P(C_{j} | A) = \frac{P(C_{j}) P(A | C_{j})}{\sum_{i=1}^{k} P(C_{i})P(A|C_{i}) } $$
위 식과 같이 베이즈 정리는 k개의 사건 $C_1, C_2, C_3, ... , C_{k}$의 확률, 그리고 사건 ${C_j}$가 주어진 어떤 사건 $A$의 조건부 확률 $P(A | C_{j})$을 이용함으로써 사건 $A$가 주어진 사건 $C_{j}$의 조건부 확률 $P(C_{j} | A)$ 을 구할 수 있게 하는 유용한 정리입니다.
식만 본다면 왜 이렇게 구하나 싶겠죠?
이는 우리가 구하고자 하는 확률 $P(C_{j} | A)$ 이 현실적으로 구하기 어려운 상황일 때 도움을 줍니다.
우선 베이즈 정리의 유도 과정을 한번 살펴보죠.

증명 과정 자체는 어렵지 않습니다.
조건부 확률에서 다루었던 곱셈법칙, 즉 Marginal Prob. 과 Conditional Prob.의 곱이 Joint Prob.이 됨을 알고 있다면 어떤 사건 A의 확률을 이들의 합으로 표현할 수 있습니다.
$$ P(A) = \sum_{i=1}^{k} P(C_{i})P(A | C_{i})$$
이를 총 확률의 법칙(Law of Total Probability)이라고 하는데요.
이것이 가능한 이유는 베이즈 정리를 정의할 때 k개의 사건 $C_i$들을 Sample Space의 Partition 이라고 가정했기 때문입니다.
그러므로 임의의 사건 $A$는 당연히 Sample Space의 subset일 거고, k개의 $C_{i}$들은 Mutually Exclusive하고 Exhaustive한 set들이니 사건 $A$와 joint set도 존재할 것이며, 각 $C_{i}$들과 $A$의 joint set은 서로 disjoint하겠죠.
$$ A = (A \cap C_{1}) \, \cup \, (A \cap C_{2}) \, \cup \, \cdots \, \cup \, (A \cap C_{k}) $$
이러한 가정 덕분에 $P(A)$는 k개의 Marginal Prob. 과 Conditional Prob.의 곱의 합으로 이루어질 수 있는 겁니다.
이를 총확률의 법칙(Law of Total Probability)이라고 합니다.
다시 베이즈 정리의 공식으로 돌아가보죠.
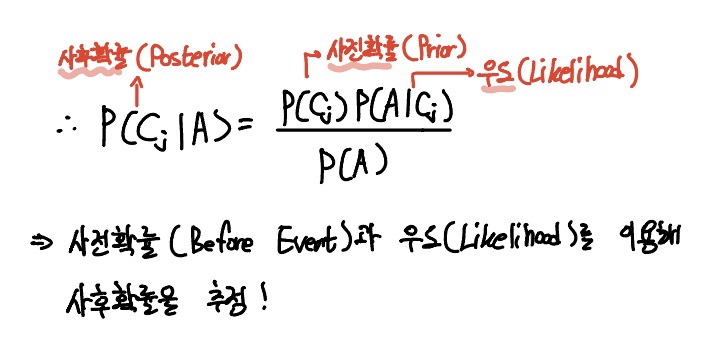
그래서 이 베이즈 정리의 좌변, 즉 우리가 구하고자 했지만 현실적으로 계산하기 어려운 확률을 사후확률(Posterior Prob.) 이라고 하고,
우변을 사전확률(Prior Prob.) $P(C_j)$과 현실적으로 계산하기 용이한 우도(Likelihood) $P(A | C_{j})$ 의 곱으로 표현할 수 있습니다.
$$ P(C_{j} | A) = \frac{ P(C_{j} ) \, P(A|C_{j}) }{ P(A)} $$
그래서 베이즈 정리의 핵심은 사전확률과 우도를 이용해 사후확률을 추정하는 것이죠!
문제를 통해 베이즈 정리의 개념을 적용해봅시다.

기계 $A_1, A_2, A_3$ 3대의 각 생산량이 전체 생산량의 10%, 50%, 40%을 생산한다고 가정합시다.
그리고 각 기계의 고장률은 1%, 3%, 4%라고 주어졌다고 하죠.
이때 어떤 사건 $B$ 를 "한 제품을 골랐더니 그게 불량품인 사건", 즉 불량품을 생산할 사건이라고 하죠.
그렇다면 주어진 문제는 "불량품을 생산했는데 $P(B)$, 이 생산된 제품이 기계 $A_1$에서 생산되었을 확률 $P(A_{1} \cap B)$"을 구하는 것이라고 합시다.
그러므로 우리가 구하고자 하는 값 사후확률(Posterior)은 $P( A_{1} | B )$ 라고 할 수 있겠군요.
한번 $P( A_{1} | B )$을 구해봅시다.

각 기계가 생산하는 생산량의 비율은 각 사건의 사전 확률이라고도 할 수 있습니다.
$$ P(A_{1}) = 0.1, P(A_{2}) = 0.5, P(A_{3}) = 0.4 $$
그리고 해당 기계가 불량품을 생산할 확률은, 다시 말하면 "해당 기계의 제품을 하나 집었는데, 이 제품이 불량품인 사건의 확률"이라고 할 수 있겠네요.
$$ P(B|A_{1}) = 0.01, P(B | A_{2}) = 0.03, P(B | A_{3}) = 0.04 $$
이는 우도라고 할 수 있습니다.
그러므로 Law of Total Prob.에 의해 P(B)는 사전 확률과 우도의 곱을 모두 더한 값으로 구할 수 있습니다.
$$ P(B) = \sum_{i=1}{3} P(A_{} \cap B) = \sum_{i=1}{3} P(A_{i})P(B | A_{i}) = 0.032 $$
$$ \therefore P(A_{1} | B) = \frac{P(A_{i} \cap B)}{P(B)} = \frac{0.1 \times 0.01}{0.032} \approx 0.031 $$
이를 통해 $P( A_{1} | B )$ 를 어렵지 않게 구할 수 있습니다.
이해가 쏙쏙 되시죠?
한번 헷갈릴만한 개념을 짚고 넘어가겠습니다.

사건 A가 발생하는 것이 사건 B의 발생에 영향을 미치지 않는다고 가정합시다.
만약 고객이 맥주를 구매할 때 오징어도 같이 구매하는 Case를 생각해본다면, 이는 충분히 관련이 있는 case임을 알 수 있겠죠. 안주로 먹으니깐요.
그러나 고객이 맥주를 구매할 때 "수세미"도 같이 구매하는 사건은 합리적으로 생각했을 때 명확한 관련이 있을 것 같진 않습니다. 그냥 없다고 가정합시다!
그러므로 맥주를 구매하는 사건은 수세미를 구매하는 사건에 영향을 미치지 않습니다.
우리는 이를 독립 사건(Independent Event)라고 합니다.

만약 $P( B | A ) = P(B)$ 가 성립한다면, 사건 A와 B는 독립입니다.
따라서 A와 B의 Joint Probability가 각 사건의 확률을 서로 곱한 것과 같음을 유도할 수 있습니다.
$$ P(A \cap B) = P(A) \times P(B) $$
흔히 하시는 실수 중에 하나가 독립과 배반을 헷갈려하는 경우인데요.

서로 사건의 발생에 영향을 미치지 않는다고 해서 교집합이 없는 게 아닙니다.
즉 독립은 교집합이 각 사건을 곱한 것으로 표현되는 거고,
배반은 교집합이 공집합, 즉 동시에 발생하지 않는 겁니다.
위 예시를 다시 빌려오면,
고객이 맥주를 사는 것과 수세미를 사는 게 서로 "발생에 영향을 끼치지 않는다"면, 이는 독립입니다.
당연히 별 이유 없이 맥주랑 수세미를 동시에 구매할 수는 있겠죠. 다만 이 구매엔 어떠한 인과관계가 없겠지만요.
다만 맥주를 사는 것과 동시에 집에서 설거지를 하는 사건은 발생할 수 없습니다.
이 경우엔 교집합이 존재하지 않으므로 배반 사건이라고 할 수 있습니다. 이해가 되시죠?
어쩌다보니 포스팅이 길어졌네요.
다음 포스팅에서는 확률변수(Random Variable)와 확률변수의 분포를 알려주는 확률함수에 대해 다뤄보겠습니다.
감사합니다.
잘 읽으셨다면 게시글 하단에 ♡(좋아요) 눌러주시면 감사하겠습니다 :)
(구독이면 더욱 좋습니다 ^_^)
* 본 블로그는 학부생이 운영하는 블로그입니다.
따라서 포스팅에 학문적 오류가 있을 수 있으며, 이를 감안해서 봐주시면 감사하겠습니다.
- 간토끼(DataLabbit)
- B.A. in Economics, Data Science at University of Seoul
'Statistics > Mathematical Statistics' 카테고리의 다른 글
| [수리통계학] 이산확률변수와 연속확률변수(Discrete and Continuous Random Variable) (2) | 2023.10.05 |
|---|---|
| [수리통계학] 확률변수(Random Variable ; R.V.) (2) | 2023.09.14 |
| [수리통계학] 불의 부등식(Boole's Inequality) (0) | 2023.07.21 |
| [수리통계학] 확률의 성질과 포함-배제 원리(Inclusion-Exclusion Principle) (0) | 2023.07.19 |
| [수리통계학] 확률집합함수(Probability Set Function) (0) | 2023.07.07 |
