Review
참고 포스팅 :
2020/05/18 - [Statistics/Basic Statistics] - [기초통계학] 확률변수와 기댓값, 분산
[기초통계학] 확률변수와 기댓값, 분산
Review 참고 포스팅 : 2020/05/15 - [Statistics/Basic Statistics] - [기초통계학] 기술통계학(Descriptive Statistics)기초 2 - 모집단과 표본집단 with 모수&통계량 [기초통계학] 기술통계학(Descriptive Stat..
datalabbit.tistory.com
안녕하십니까, 간토끼입니다.
이전에 가볍게 확률변수에 대해서 다뤄봤었는데요.
이번 포스팅에서는 확률변수의 분포 형태를 나타내는 데 사용되는 확률밀도함수(Probability Density Function)와 확률분포함수(Probability Distribution Function)를 다뤄보도록 하겠습니다.

이전에 확률변수를 다룰 때 크게 두 가지로 구분하였습니다.
먼저 직접 셀 수 있는 이산확률변수(Discrete Random Variable)가 있었죠.

만약 확률변수 X가 동전의 앞면이 나온 횟수라고 하면,
이 X가 가질 수 있는 값은 0, 1, 2, 3 등 유한개(Finite)일 수도 있고,
동전을 던지는 시행을 무수히 반복한다고 가정하면 0, 1, 2, 3 ... 등 셀 수 있는 무한개인 가산무한일 수 있습니다.
우리는 이러한 변수를 이산확률변수라고 정의하였습니다.
다른 하나는 셀 수 없는 변수인 연속확률변수(Continuous Random Variable)이었죠.
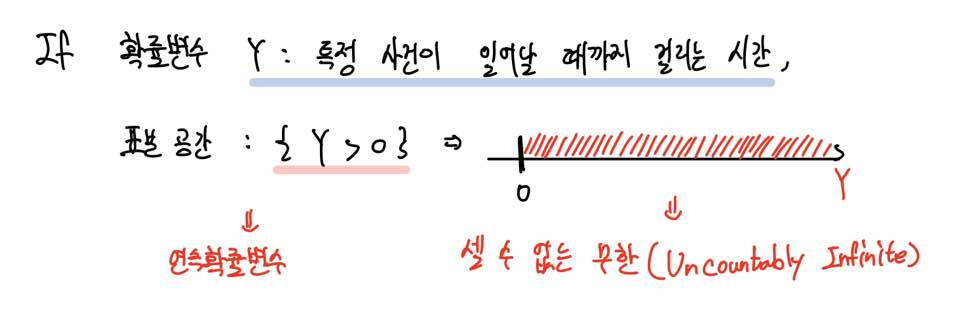
만약 확률변수 Y를 특정 사건이 일어날 때까지 걸리는 시간(time)이라고 가정하면,
확률변수 Y가 가질 수 있는 값은 특정한 값이 아닌 영역으로 표현이 될 것이며, 이 영역은 셀 수 없는 무수히 많은 값을 포함하겠죠.
우리의 직관상 시간도 30분! 1시간! 이렇게 셀 수 있는 값으로 표현할 수 있는 게 아니냐고 물을 수 있지만,
누구든지 정확히 30분을 찍으라고 하면 아마 미세한 차이로 약간씩 다를 겁니다.
왜냐하면 30분 0.00000000000000....00000000000......1.....000 등 아주 미세하게 찍기엔 이 소수의 끝자리가 어디까지 있을지 모르기 때문이죠.
누구는 30분 0.000001초가 30분이라고 하고, 누구는 30분 0.00000....00000...0001초가 30분이라고 할 수도 있겠죠?굳이 비유하자면 그렇습니다.
각설하고 확률변수가 가질 수 있는 값의 범위가 위와 같이 실직선상의 어떤 구간인 경우, 우리는 이를 연속확률변수라고 정의하였습니다.
그래서 이러한 확률변수의 분포를 알 수 있다면, 확률변수가 특정한 값(혹은 범위)을 가질 때의 확률을 알 수 있을 겁니다.
예를 들어 반 아이들의 시험 성적이 70점에서 80점 사이일 확률을 알고 싶다면, 반 아이들의 시험 성적에 대한 분포를 알고 있으면 되겠죠!
그러한 맥락에서 출발한 것이 확률밀도함수(Probability Density Function, PDF)입니다.
먼저 이산확률변수부터 살펴볼까요?

이산확률변수의 확률밀도함수는 확률질량함수(Probability Mass Function)이라고 합니다.
핵심은 '확률' 이므로 모든 실수 x에 대하여 당연히 0보다 크거나 같아야 하며,
확률변수가 가질 수 있는 값에 대해서는 항상 0보다 커야겠으며 그 합은 1이 되어야 할 것입니다.
(1)번에서는 모든 실수라고 정의하였으니까 확률변수가 가질 수 없는 값이라면 확률이 0이 될 수 있지만,
확률변수가 가질 수 있는 값에 대해서는 0보다 커야한다는 것을 잘 기억하시면 됩니다.
그리고 임의의 값 x에 대한 확률은 확률질량함수의 값과 같습니다.시험 성적이 30점일 확률은 f(30)의 값을 구하면 된다는 것이죠.
연속확률변수도 크게 다르지는 않으나 기호가 약간 차이가 있습니다.

연속확률변수는 셀 수 없으므로, 가능한 값 하나하나에 확률을 부여하지 않고 구간에 확률을 부여합니다.
즉 임의의 실수 x에 대하여, x의 확률은 항상 0이 됩니다.
또한 구간의 넓이를 구하는 것이므로, 적분을 이용해야 한다는 것을 명심해야 겠습니다.
두 변수의 차이는 결국 합을 나타내는 방법이 ∑(sigma) 인지, ∫(integral)인지의 차이로 정리할 수 있습니다.
또한 확률변수의 분포를 표현하는 다른 방법으로는 확률밀도함수를 누적하여 구할 수 있는 확률분포함수, 다른 말로는 누적분포함수(Cumulative Distribution Function, CDF)가 있습니다.

누적분포함수는 확률변수가 임의의 값 x 이하인 모든 값을 가질 확률을 누적함으로써 정의됩니다.
이산형일 경우 sigma를 이용한 합을, 연속형일 경우 integral을 이용한 합으로 표현할 수 있겠죠.

그렇기에 확률변수가 구간 (a, b] 사이의 값을 가질 확률은 누적분포함수를 이용하여 위와 같이 구할 수 있습니다.
한번 직접 풀어보죠!
1. X가 이산확률변수일 경우

확률변수 X가 동전을 3회 독립반복하여 던졌을 때 나온 앞면의 수라고 가정하면, X가 가질 수 있는 값은 0, 1, 2, 3이며 이에 대응되는 확률은 위와 같습니다.
(확률은 우측에 있는 식에 의해 도출됐으며 추후 이항분포를 다룰 때 나올 예정입니다.)

위 확률질량함수를 그래프로 표현하면 좌측과 같으며, 누적분포함수로 표현하면 우측과 같습니다.
누적분포함수가 가우스 함수와 같이 표현이 됐지만, 사실 위 문제에서는 X가 정수이므로 점으로 표현돼도 무방할 것입니다.
각설하고 확률변수가 구간 사이의 값을 가질 확률을 CDF를 이용해 풀어보면 다음과 같습니다.

P(1 < X <= 2)일 확률은 결국 P(X=2)와 같으며, 이는 누적분포함수의 뺄셈과 같음을 알 수 있습니다.
2. X가 연속확률변수일 경우
이번엔 연속확률변수의 문제를 풀어보죠.

음... X가 0보다 작은 범위에서는 확률이 0이고, 0보다 큰 범위에서는 함수 형태로 표현이 됐습니다.
먼저 상수 c의 값을 구하고, 확률밀도함수를 적분하여 누적분포함수 꼴로 나타낼 수 있어야 하겠죠?

풀이는 다음과 같습니다.
마찬가지로 확률변수 X가 구간 1과 2 사이에 속할 확률을 누적분포함수의 뺄셈으로 나타낼 수 있습니다.
위 문제를 통해 알 수 있는 사실은 연속확률변수 X의 PDF가 f(x)이고, CDF가 F(x)라면,
PDF f(x)는 F(x)를 미분함으로써 얻을 수 있다는 것입니다.
증명은 그냥 누적분포함수의 식을 x에 대하여 미분하면 f(x)가 나옵니다. 참 쉽죠?
적다보니 포스팅이 조금 길어졌네요.
다음 포스팅에서는 이산확률변수의 대표적인 분포인 베르누이 분포와 이항분포에 대해서 다루겠습니다.
감사합니다.
잘 읽으셨다면 게시글 하단에 ♡(좋아요) 눌러주시면 감사하겠습니다 :)
(구독이면 더욱 좋습니다 ^_^)
- 간토끼(DataLabbit)
- University of Seoul
- Economics, Big Data Analytics
'Statistics > Basic Statistics' 카테고리의 다른 글
| [기초통계학] 이산확률분포 - 베르누이 분포, 이항분포 (4) | 2020.09.08 |
|---|---|
| [기초통계학] 순열과 조합(Permutation and Combination) (0) | 2020.09.07 |
| [기초통계학] 체비셰프 부등식(Chebyshev Inequality) (3) | 2020.06.24 |
| [기초통계학] 마르코프 부등식(Markov Inequality) (2) | 2020.05.26 |
| [기초통계학] 확률(Probability) 3 - 베이즈 정리(Bayes’ theorem) (2) | 2020.05.25 |
