[행렬대수학] 행렬식(Determinant) 3 - 역행렬(Inverse Matrix)과 행렬식의 관계

Review

참고 포스팅 : 

2020.09.05 - [Statistics/Matrix Algebra] - [행렬대수학] 행렬식(Determinant) 1 - 행렬식의 개념

[행렬대수학] 행렬식(Determinant) 1 - 행렬식의 개념

2023.11.01 - [Statistics/Matrix Algebra] - [행렬대수학] 행렬식(Determinant) 2 - 행렬식의 유용한 성질과 수반행렬(Adjoint)

[행렬대수학] 행렬식(Determinant) 2 - 행렬식의 유용한 성질과 수반행렬(Adjoint)

---

안녕하십니까, 간토끼입니다.

 

행렬식 시리즈의 3번째 포스팅입니다. 생각보다 다루다보니 욕심이 생겨서 총 5부작으로 진행할 예정입니다.

 

지난 포스팅까진 행렬식의 성질에 대해서 다뤄보았으며, 특히 포스팅의 마지막엔 수반 행렬(Adjoint)의 개념을 소개하며 마무리했었죠.

 

이번 포스팅에서는 새로운 개념인 역행렬(Inverse Matrix)에 대해 소개하고, 이 역행렬과 행렬식이 어떤 관계가 있는지에 대해 다뤄보겠습니다.

 

 

---

 

1. 역행렬(Inverse Matrix)의 개념

 

역행렬에 대해서 알아보기 전에, 가볍게 다음과 같이 간단한 미지수가 1개인 방정식을 생각해봅시다.

 

만약 $2x_{1} = 4$ 라는 방정식이 있다면, 이 방정식의 해 $x_{1}$ 는 어떻게 구할 수 있을까요?

 

간단합니다.

바로 계수의 역수인 $\frac{1}{2}$ 을 양변에 곱해줌으로써 해를 구하면 되겠죠.

 

 

그러면 미지수가 2개인 방정식의 해는 어떻게 구할까요?

우선 미지수가 2개이니, 2개의 식이 필요하겠죠.

 

 

연립방정식을 이용해도 되겠지만, 우리는 행렬의 개념에 대해 배우면서 위 선형시스템(linear system)을 다음과 같이 표기할 수 있다고 했습니다.

 

$$ \begin{bmatrix} 2 & 3 \\ 1 & 2 \end{bmatrix} \, \begin{bmatrix} x_{1} \\ x_{2} \end{bmatrix} \, = \, \begin{bmatrix} 13 \\ 8 \end{bmatrix} $$

 

 

여기서 방정식의 계수 부분을 행렬 $A$ 라고 할 수 있겠으며, 이는 계수 행렬(Coefficient Matrix)이라고 했습니다.

 

그러면 방정식의 해(solution) $x$ 는 행렬 $A$ 를 이용해서 어떻게 구할 수 있을까요?

 

 

 

우리가 배운 개념을 활용한다면 행렬 $A$ 를 가우스 소거법이나 가우스-조던 소거법을 이용해서 해를 구할 수 있겠죠.

 

하지만 위에서 언급한 '계수의 역수를 곱하는' 방법을 사용해볼 수도 있지 않을까요?

 

만약 양변에 $A$ 의 역수를 곱합으로써 $ \frac{1}{A} \,Ax = \frac{1}{A} \, b $ 라는 식이 가능하다면,

우리가 찾고자 하는 solution vector $x$ 는 $\frac{1}{A} \, b$ 와 같지 않을까요?

 

 

결론부터 말하자면 $A$ 는 행렬(Matrix)이므로, 상수(scalar)가 아니기에 분수 꼴로 표현할 수 없습니다.

그렇지만 이런 관점으로 접근해보는 것은 충분히 합리적인 접근 방법이라고 생각합니다.

 

 

 

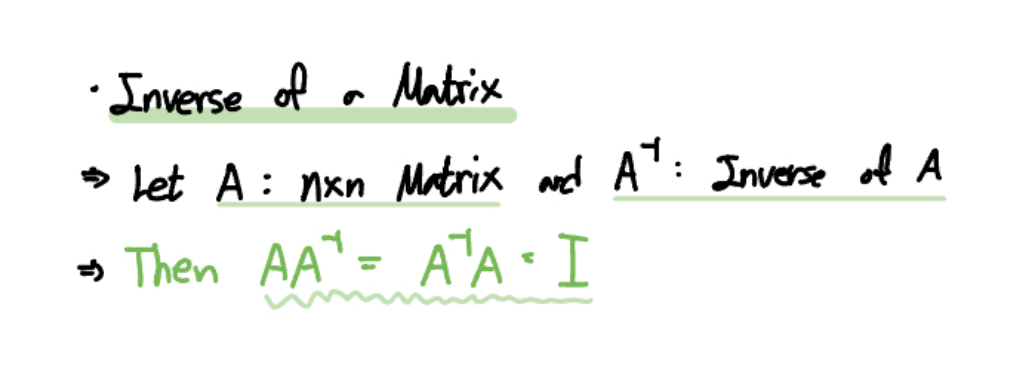
역행렬(Inverse Matrix)은 이러한 관점을 만족하는 개념입니다.

 

만약 어떤 정방행렬(Square Matrix) $A$ 가 있다고 가정합시다.

그리고 다음을 만족하는 행렬 $A^{-1}$ 을 행렬 $A$ 의 역행렬이라고 정의합니다.

 

$$ A\,A^{-1} = A^{-1}\,A = I $$

 

 

직관적으로 어떤 상수 $k$ 와 이 상수의 역수 $\frac{1}{k}$ 를 곱해주면 1이 되는 것과 유사한 개념입니다.

 

그리고 상수 $k$ 의 우측이든 좌측이든 상수의 역수 $\frac{1}{k}$ 를 곱해주면 항상 1이 되죠.

 

행렬의 관점에서는 이를 right inverse, left inverse 라고 합니다.

 

 

그리고 위 행렬 $A$ 를 다음과 같이 가역행렬(Invertible Matrix) 이라고 합니다.

또한 이런 가역행렬은 항상 Non-singular Matrix 입니다.

 

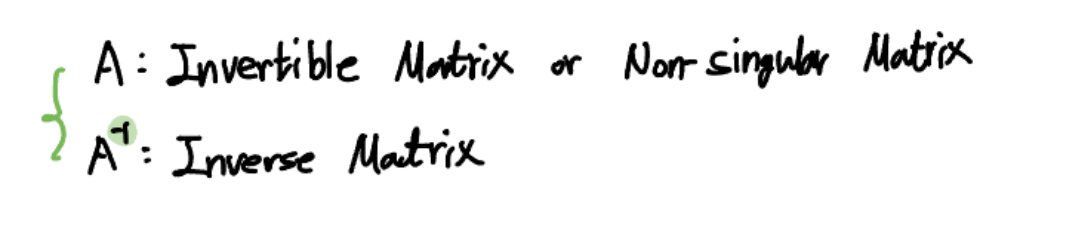
그러면 임의의 가역행렬에 대해서 역행렬은 항상 유일하게 존재할까요?

 

네, 맞습니다. 항상 유일한 역행렬을 갖습니다.

 

 

만약 가역행렬 $A$ 의 Left Inverse를 $C$ 라고 하고, Right Inverse를 $B$ 라고 합시다.

그러면 역행렬의 정의에 의해 $CA = I$ 와 $AB = I$ 는 항상 성립하겠죠.

 

$$ Then \,\,\, C = CI =C(AB) = (CA)B = IB = B , \,\, \therefore \,\, C = B = A^{-1} $$

 

위 과정을 통해 가역행렬의 역행렬은 항상 유일함을 증명할 수 있습니다.

 

 

간단한 2차원 행렬을 통해 가역행렬과 그 역행렬의 곱이 Identity Matrix가 되는지 한번 보도록 하죠.

 

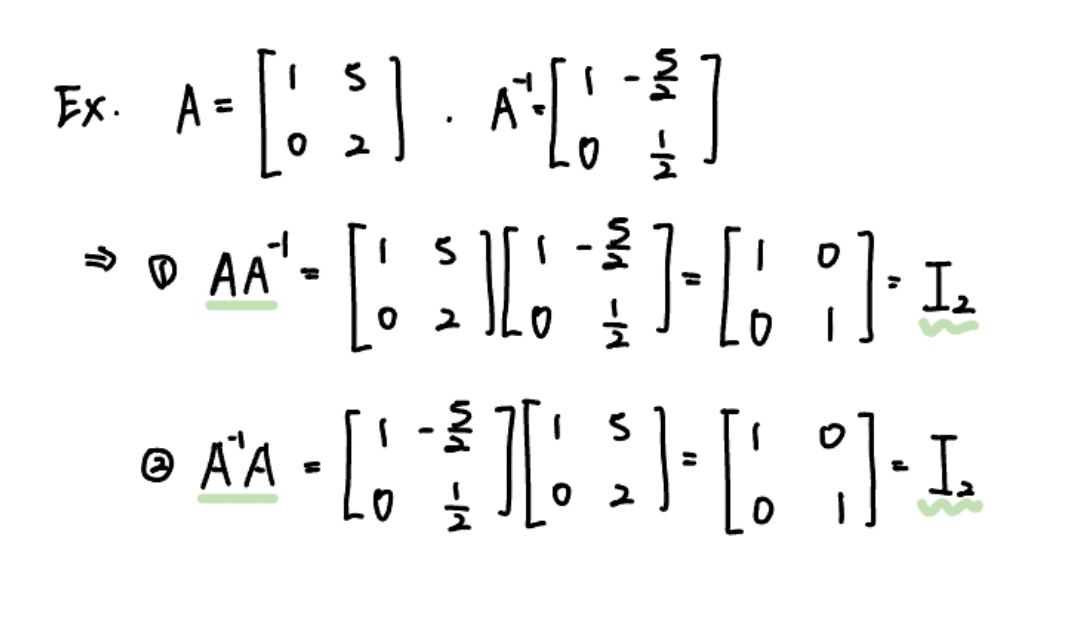
우리는 역행렬을 구하는 방법을 아직 모르지만, $ A = \begin{bmatrix} 1 & 5 \\ 0 & 2 \end{bmatrix} $ 의 역행렬이 $ A^{-1} = \begin{bmatrix} 1 & -\frac{5}{2} \\ 0 & \frac{1}{2} \end{bmatrix} $ 라고 합시다.

 

그러면 위 과정을 통해 앞에서 곱하든, 뒤에서 곱하든 항상 Identity Matrix 가 됨을 알 수 있습니다.

 

 

---

 

2. 역행렬(Inverse Matrix) 구하기

 

이번에는 직접 역행렬을 구해봅시다.

 

역행렬을 구하는 방법은 크게 2가지로 나눌 수 있습니다.

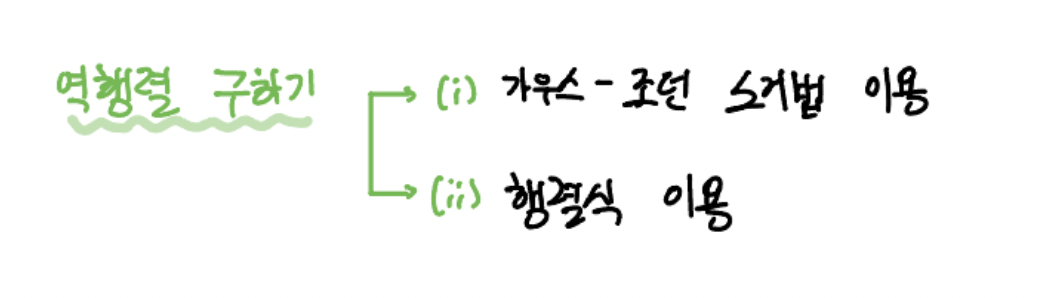
첫 번째는 가우스-조던 소거법(Gauss-Jordan Elimination)을 이용하는 것이고,

두 번째는 행렬식(Determinant)을 이용하는 것입니다.

 

하나씩 살펴보죠.

 

 

 

(1) 가우스-조던 소거법(Gauss-Jordan Elimination) 이용

 

예시로 2차원 행렬 $ A = \begin{bmatrix} 4 & 3 \\ 2 & 1 \end{bmatrix} $ 을 가정합시다.

그리고 이 행렬은 역행렬이 존재하는 가역행렬입니다.

 

가역행렬이라는 사실은 행렬 $A$ 의 행렬식이 0이 아님을 보임으로써 쉽게 확인할 수 있는데요.

 

행렬식을 이용한 방법에서 이 개념을 다룰 예정이니 우선 기억만 해둡시다.

 

 

 

각설하고, 먼저 행렬 $A$ 와 2차원 Identity Matrix $I$ 를 결합한 확장 행렬(Extended Matrix)의 형태로 만들어줍니다.

확장 행렬은 첨가 행렬(Augmented Matrix)와 같은 말입니다.

 

그리고 이 확장 행렬에서 행렬 $A$ 를 기본 행 연산(Elementary Row Operarion)을 통해 Identity Matrix 로 만들어주면 됩니다.

 

즉 Gauss-Jordan 소거법을 이용해서 RREF (기약 행 사다리꼴 형태) 로 만들어주는 거죠!

 

 

그러면 위와 같이 최초 $ [\,A \,|\, I \,] $ 였던 행렬이 $ [\,I \,|\, A^{-1} \,] $ 의 꼴로 바뀐 것을 알 수 있습니다.

 

이렇게 가우스-조던 소거법을 이용해서 역행렬을 구해줄 수 있습니다.

 

근데 좀 번거롭네요.

 

만약 3차원, 혹은 4차원 등 차원이 커진다면 역행렬을 가우스-조던 소거법으로 계산하는 것은 다소 부담이 될 것 같습니다.

 

 

그럴 땐 행렬식을 이용하는 방법이 대안이 될 수 있습니다.

 

 

 

 

2. 행렬식(Determinant) 이용

 

우선 행렬식을 구해보면 -2 가 나옴은 쉽게 이해하실 수 있을 것 같습니다.

 

$A$ 의 역행렬 $A^{-1}$ 은 다음과 같이 쓸 수 있습니다.

 

$$ A^{-1} = \frac{1}{det \, (A)} \,\, adj\,(A) $$

 

여기서 $adj \, (A)$ 은 지난 포스팅에서 다루었던 수반 행렬(Adjoint)가 되겠죠.

 

 

그리고 $\frac{1}{det \, (A)}$ 을 곱해주는데요.

여기서 왜 가역행렬의 행렬식이 0이 되면 안 되는지 이유를 알 수 있습니다.

 

만약 행렬식이 0이라면 $\frac{1}{0}$ 은 정의할 수 없으므로 역행렬 $A^{-1}$ 은 존재할 수 없죠.

 

그러므로 역행렬이 존재하는 가역행렬이 되려면, 이 행렬의 행렬식은 항상 0이 되어서는 안 됩니다.

 

 

그러면 한번 행렬식과 adjoint를 이용해 역행렬을 구해봅시다.

 

 

지난 포스팅에서 adjoint 의 개념을 보고 오셨다면 어렵지 않을 거라 생각합니다.

 

어쨌든 가우스-조던 소거법을 이용하든, 행렬식을 이용하든 역행렬은 동일함을 보일 수 있습니다.

 

둘 중 편한 방법을 사용하시면 되지만 ... 4차원 이상으로 행렬이 커지게 되면 손으로 역행렬을 구하는 것은 꽤나 어려울 것 같습니다. (저는 계산이 약해서 무조건 실수를 합니다 ... ㅜㅜ)

 

728x90

 

그나저나 재밌는(?) 사실들이 보이는 것 같습니다.

 

가우스-조던 소거법을 이용하면 가역행렬은 항상 RREF, 즉 Identity Matrix 가 된다는 건데요.

 

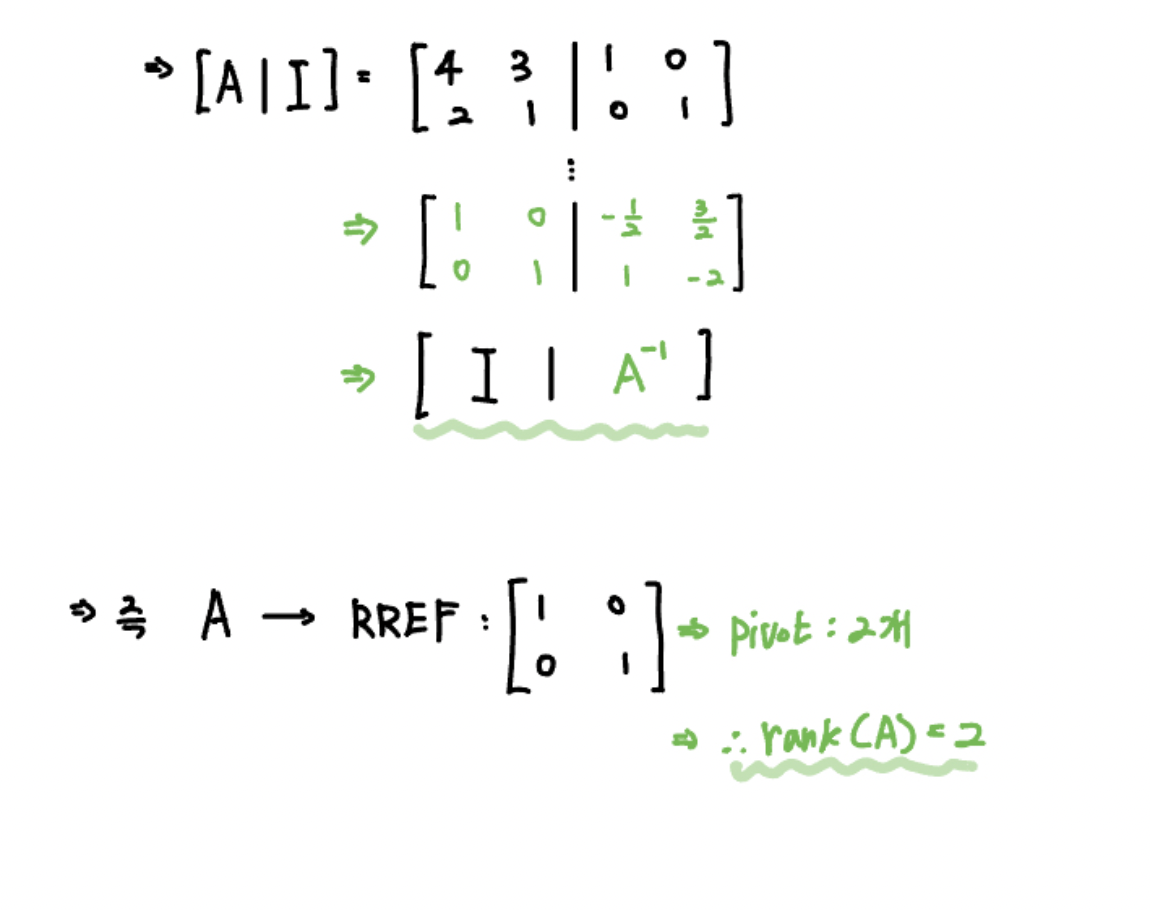
기억하실진 모르겠지만, 가우스-조던 소거법 포스팅에서 간단하게 랭크(rank)의 개념을 다뤘었습니다.

2020.07.01 - [Statistics/Matrix Algebra] - [행렬대수학] 가우스-조던 소거법(Gauss-Jordan Elimination)

[행렬대수학] 가우스-조던 소거법(Gauss-Jordan Elimination)

 

즉 rank는 pivot의 개수를 의미하죠. 그러므로 위 가역행렬 $A$ 의 rank는 2이고, 이는 $A$ 의 차원(Dimension)인 $n=2$ 과 같음을 알 수 있습니다.

 

 

생각해보면 가역행렬의 행렬식은 항상 0이 아닌 상수잖아요?

 

그러면 역행렬을 갖는 어떤 n x n 가역행렬은 항상 행렬식이 0이 아닌 상수이고, rank(A) = n 을 만족하며 유일한 역행렬을 갖는 행렬이겠네요?

 

 

이렇듯 임의의 행렬이 가역행렬(Invertible Matrix)이라면, 다음과 같은 명제는 모두 동치입니다.

 

추가로 가역행렬 $A$ 의 전치행렬 $A^{T}$ 또한 가역행렬입니다.

 

 

사실 위 사실들 말고도 중요한 사실들이 많습니다.

 

rank(A) = n 이라는 것은 행렬 A의 모든 column은 linearly independent 한다는 것을 의미하고,

이는 행렬의 column들이 $R^{n}$ 의 basis가 되어 행렬의 column space가 $R^{n}$ 이 됨을 의미합니다.

 

뿐만 아니라 고윳값(Eigen Value)의 개념과도 연결할 수 있고요.

 

하지만 아직 이런 개념들을 다루기엔 시기상조이니, 조만간 다루도록 하겠습니다.

 

 

다음 포스팅에서는 행렬식을 이용해 행렬의 해(solution)을 구하는 방법인 크래머 룰(Cramer's Rule)에 대해 다뤄보도록 하겠습니다.

 

 

 

감사합니다.

 

잘 읽으셨다면 게시글 하단에 ♡(좋아요) 눌러주시면 감사하겠습니다 :)

(구독이면 더욱 좋습니다 ^_^)

 

* 본 블로그는 학부생이 운영하는 블로그입니다.

따라서 포스팅에 학문적 오류가 있을 수 있으며, 이를 감안해서 봐주시면 감사하겠습니다.

---

- 간토끼(DataLabbit)

- B.A. in Economics, Data Science at University of Seoul