Review
참고 포스팅 :
[수리통계학] 확률변수의 기댓값(Expectation of Random Variable)
Review참고 포스팅 :2023.09.14 - [Statistics/Mathematical Statistics] - [수리통계학] 확률변수(Random Variable ; R.V.) [수리통계학] 확률변수(Random Variable ; R.V.)Review # 해당 포스팅은 KOCW 김충락 교수님의 수리통계
datalabbit.tistory.com
# 해당 포스팅은 KOCW 김충락 교수님의 수리통계학 강의와 Hogg의 수리통계학개론(Introduction to Mathematical Statistics)를 기초로 작성되었습니다.
안녕하십니까, 간토끼입니다.
지난 포스팅에서는 확률변수의 중심 경향을 나타내는 기댓값(Expectated Value)에 대해서 다뤘었는데요.
이번 포스팅에서는 좀 더 나아가 확률변수의 특성을 알게 해주는 적률(Moment), 그리고 이를 생성하는 함수인 적률생성함수(Moment Generating Function; MGF)에 대해 다뤄보겠습니다.

지난 포스팅에서 다루었던 기댓값을 다시 한번 살펴보고 가겠습니다.

확률변수의 기댓값은 다음과 같이 정의했었습니다.
확률변수의 원소 값 $x$와 그에 대응하는 확률 $p(x)$를 곱한 값을 모두 더해준다고 했죠.
이는 각 $x$에 대응되는 확률 $p(x)$가 일종의 가중치(weight) 역할을 하는 가중평균(Weighted Average)과 같다고 했었습니다.
다만 그렇기에 일반적으로 사용하는 "산술평균"과는 다름을 인지해야 한다고 강조했었습니다.
우리는 앞으로 이 확률분포의 중심 경향을 나타내는 기댓값 $E(X)$를 평균(Mean) $\mu$ 라고 하겠습니다.
특별한 언급이 없으면 이 $\mu$는 $E(X)$를 의미합니다.
자 그렇다면 이 기댓값말고 확률변수의 특성을 알 수 있는 다른 지표는 없을까요?

그래서 우리는 이를 위해 적률(Moment)을 사용합니다.

Moment는 물리학에서 사용되는 용어입니다.
경제학 전공인 제가 이 포스팅을 위해 Chat GPT의 과외를 받으며 모멘트를 공부했습니다 ...
각설하고, 모멘트(Moment)는 질량과 질량의 위치(거리)를 곱한 값으로 정의합니다.
이러한 모멘트는 질량의 분포와 관련한 정보를 제공하는 지표입니다.
모멘트를 좀 더 세부적으로 제1모멘트와 제2모멘트로 나누어 보겠습니다.

제1모멘트는 무게중심을 의미합니다.
$m_i$를 i번째 물체의 질량, 그리고 $x_i$를 위치라고 하면 각 물체의 질량과 위치를 곱하여 더한 값 $\sum m_ix_i$ 을 물체의 질량의 총합 $\sum m_i$으로 나누어 주면 이 물체들의 질량 분포의 무게중심이 됩니다.
이를 제1모멘트라고 합니다.
제1모멘트의 우측 그림을 통해 직관적으로 설명하겠습니다.
4개의 물체가 있고, 각 물체의 질량을 $m_1, m_2, m_3, m_4$, 그리고 물체의 위치는 보시는 바와 같이 정렬돼있다고 하겠습니다.
쉽게 말하면 시소 위에 물체들을 정렬하고, 이 시소를 평행하게 할 무게 중심을 찾는 것이죠.
당연하겠지만 이 분포의 무게중심은 시소의 정중앙이 아닙니다. 2번째 물체의 질량 $m_2$이 보다시피 가장 크므로, 이를 고려해 좌측으로 치우쳐있음을 알 수 있죠.
제2모멘트는 회전 관성 모멘트라고 합니다.
회전 관성 모멘트는 물체의 질량 $m_i$에 회전축 $k$ 로부터 물체가 떨어진 위치를 제곱한 값 $(x_i - k)^2$을 곱하여 더한 값 $\sum m_i \times (x_i-k)^2$으로 정의합니다.
즉, 회전축으로부터 물체가 멀어질 경우, 회전 관성 모멘트는 더욱 커지게 되고, 이는 회전하는 데 더욱 많은 힘을 필요로 한다는 것을 의미합니다.
이러한 회전 관성 모멘트는 물체의 회전의 정도를 측정하는 지표입니다.
이번엔 통계학에서의 Moment를 살펴봅시다.

통계학에서 Moment는 적률이라고 합니다.
만약 $X$의 n차 제곱한 값의 기댓값을 $E(X^n)$ 이라고 하면, 이를 $\mu _n$ 이라고 하고 편의상 $X$의 n차 적률이라고 합니다.
이 적률(Moment)는 확률변수의 분포, 즉 확률분포의 특성을 설명해주는 효과적인 지표입니다.

확률변수 $X$를 어떤 양수 $h$에 대하여 $-h < t < h$를 만족하고, $e^{tX}$ 의 기댓값이 존재하는 확률변수라고 합시다.
그러면 이 확률변수 $X$의 적률생성함수(Moment Generating Function)를 $e^{tX}$의 기댓값으로 정의할 수 있습니다.
형태가 다소 신기하게 생겼죠?
이 함수가 왜 적률을 생성하는 함수라는 건지 한번 자세히 살펴보겠습니다.

적률생성함수를 전개해보겠습니다.
$e^{tX}$는 Taylor Expansion에 의해 $t=0$ 부근에서 $1 + tx + \frac{t^2 x^2}{2!} + \cdots $로 근사할 수 있습니다.
이때 $e^{tX}$에 Expectation을 씌웠으므로,
$E(1 + tx + \frac{t^2 x^2}{2!} + \cdots) = E(1) + tE(X) + \frac{t^2}{2!} E(X^2) + \cdots$라고 할 수 있습니다.
이때 앞에서 정의한 적률 $E(X^k) = \mu_k$ 를 사용하여 위 식을 다시 쓰면 다음과 같습니다.
$$ E(1) + tE(X) + \frac{t^2}{2!} \times E(X^2) + \cdots = 1 + \mu_1 t + \frac{1}{2!} \times \mu_2 t^2 + \cdots $$
그리고 위 식을 $t$에 대해서 k차 미분하고, 미분한 식에 $t = 0$ 을 대입하면 신기하게도 깔끔하게 정리됩니다.
즉 1계 미분하여 $t=0$을 대입하면 $\mu_1$을 제외한 나머지 항은 모두 0이 되고,
마찬가지로 2계 미분하여 $t=0$을 대입하면 $\mu_2$을 제외한 나머지 항은 모두 0이 됩니다.
이를 일반화하면 다음과 같습니다.

적률생성함수를 k-차 미분하여 $t=0$을 대입하면 $\mu_k = E(X^k)$인 k차 적률(moment)이 생성됩니다.
그리고 1차 적률은 기댓값과 같음을 직관적으로 이해할 수 있죠!
그래서 우리는 이 적률(Moment)을 생성하는 함수 $M_x(t)$를 적률생성함수라고 하는 겁니다.
여담이지만 만약 $X - \mu$을 j번 제곱하여 기댓값을 취한 값 $E[ (X-\mu)^j ]$ 을 j-th Central Moment(j차 중심 적률) 이라고 합니다.
그리고 여러분들이 잘 아시는 분산(Variance)는 $E[ (X - \mu)^2 ]$이므로 Second Central Moment 라고 할 수 있죠!
자 그렇다면 이 평균과 분산을 좀 더 직관적으로 이해해봅시다.
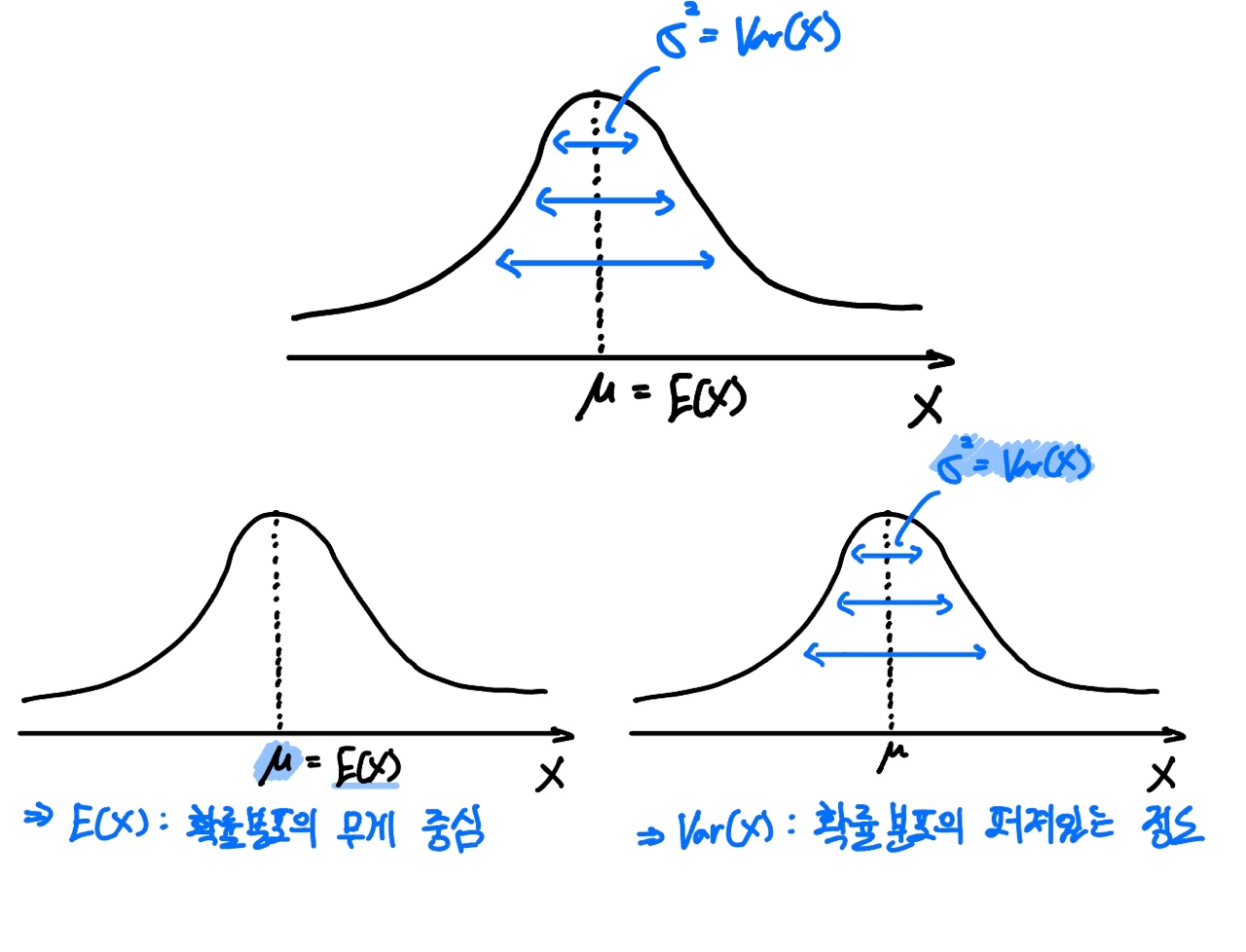
위 Central Moment의 정의에서 보셨겠지만, 분산(Variance)은 평균 $\mu$를 중심으로 얼마나 퍼져있는지를 나타내는 지표입니다.
그리고 이 평균 $\mu$는 확률분포의 중심 경향을 나타내므로, 확률분포의 무게 중심이라고도 할 수 있을 것 같습니다.
음? 보다 보니 유사한 개념이 떠오릅니다.

포스팅의 초반에서 정의한 제1모멘트와 제2모멘트의 정의와 유사한 것 같습니다.
그렇지 않나요? 한번 세부적으로 살펴보겠습니다.
먼저 기댓값(Expectation)과 제1모멘트를 비교해보겠습니다.
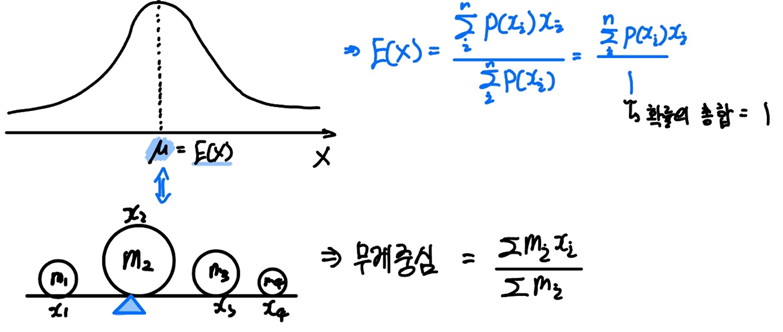
우측에 있는 기댓값의 공식을 보시면 기댓값은 확률 $p(x_i)$와 원소 $x_i$를 곱하여 더한 값 $\sum p(x_i)x_i$ 으로 정의하고 있습니다.
물론 이를 확률의 총합으로 나눠줘야 하지만, 확률의 총합은 어차피 1이기 때문에 의미가 없죠.
제1모멘트의 공식을 보시면 각 물체의 질량과 위치를 곱하여 다 더하고, 이를 질량의 총합으로 나눠줍니다.
기댓값과 제1모멘트의 공식이 같지 않나요?
기댓값은 $ \frac{\sum p(x_i)x_i}{\sum p(x_i)} $ 이고,
무게중심(제1모멘트)은 $ \frac{\sum m_i x_i}{\sum m_i}$ 이죠.
우리는 이를 통해 제1차 적률(moment)인 기댓값(Expectation)이 무게중심과 같은 개념임을 직관적으로 이해할 수 있을 것 같습니다!
즉 위에서 정의한 것처럼 확률분포에서 중심 경향을 나타내는 기댓값은, 분포의 무게중심이라고 좀 더 직관적으로 이해할 수 있다는 거죠.
이번엔 분산과 제2모멘트를 비교해보겠습니다.

분산(Variance)은 평균으로부터 얼마나 떨어져있는지를 나타내는 지표라고 했습니다.
즉 $(X-\mu)^2$의 크기에 분산의 크기가 비례함을 알 수 있죠.
마찬가지로 회전 관성 모멘트의 공식을 보면 회전축의 위치(k)로부터 얼마나 떨어져있는지에 모멘트의 크기가 비례함을 알 수 있습니다.
공식의 생김새가 같네요!
그렇다면 분산, 회전 관성 모멘트 둘다 중심으로부터 가까워지면 어떻게 바뀔까요?

예상하셨던대로 중심과 가까워질수록 공식에 의해 크기가 작아짐을 알 수 있죠.
데이터의 분포가 분포의 중심($\mu$)과 가까워질수록 퍼져있는 정도가 작다는 것이므로, 분산의 크기가 작아질 수밖에 없겠죠!
마찬가지로 물체의 위치가 회전축으로부터 가까워지면 회전 관성 모멘트는 작아지게 되고, 이는 회전을 하기 쉬워진다는 거겠죠?
팽이를 생각해보시면 팽이가 넓은 것보다 막대기에 가까울수록 회전하는 속도가 훨씬 빠름을 직관적으로 이해할 수 있으시겠죠? 같은 힘이라면 넓은 팽이보다 이쑤시개에 비슷한 팽이(?)가 훨씬 빠르게 회전하잖아요.
이렇듯 물리학, 통계학 모두 Moment와 관련된 개념은 양의 중심과 퍼짐에 대한 정보를 제공하고, 이를 통해 해당 분야에서의 중요한 특성을 파악할 수 있습니다.
적률(Moment)의 이해를 돕고자 물리학에서의 모멘트 개념을 가져왔는데, 부정확한 설명을 제공했을 수도 있을 것 같습니다.
혹여나 물리학에서의 비유에 오류가 있다면 가감없이 댓글로 지적해주세요. (물리라고는 고등학교 필수 물리학 수업 때 들어본 게 전부입니다 ... )
마지막으로 MGF의 유일성에 대해 다뤄보겠습니다.

각 MGF를 갖는 확률변수 $X, Y$를 가정합시다.
이때 두 확률변수의 누적분포함수 cdf가 같다면, 두 확률변수의 MGF 또한 같습니다.
확률변수의 cdf는 확률변수의 분포를 의미하잖아요?
즉 cdf가 같다는 것은 확률변수의 분포가 같다는 것이고, 이러한 확률변수의 mgf도 같다는 것은 확률변수의 mgf는 유일하게 정의됨을 의미합니다.
즉 같은 mgf를 공유하는 확률변수는 하나밖에 정의되지 않습니다.
물론 그렇다고 모든 확률변수가 mgf를 갖는 것은 아닙니다. (반례는 포스팅이 너무 길어져서 생략 ... )mgf를 갖지 않는 확률변수도 있습니다. mgf가 까다로운 변수도 있고요.
그럼에도 확률변수의 적률생성함수를 알 수 있다면, 기댓값뿐만 아니라 확률변수의 분산, 그리고 왜도, 첨도 등 분포의 특성을 알 수 있는 지표들을 손쉽게 구할 수 있습니다.
감사합니다.
잘 읽으셨다면 게시글 하단에 ♡(좋아요) 눌러주시면 감사하겠습니다 :)
(구독이면 더욱 좋습니다 ^_^)
* 본 블로그는 학부생이 운영하는 블로그입니다.
따라서 포스팅에 학문적 오류가 있을 수 있으며, 이를 감안해서 봐주시면 감사하겠습니다.
- 간토끼(DataLabbit)
- B.A. in Economics, Data Science at University of Seoul
'Statistics > Mathematical Statistics' 카테고리의 다른 글
| [수리통계학] 두 확률변수의 분포와 기댓값(Distributions and Expectation of Two Random Variables) (1) | 2023.10.31 |
|---|---|
| [수리통계학] 컨벡스 함수와 젠센 부등식(Convex and Jensen's Inequality) (0) | 2023.10.23 |
| [수리통계학] 확률변수의 기댓값(Expectation of Random Variable) (1) | 2023.10.14 |
| [수리통계학] 확률변수의 변환(Transformation) (10) | 2023.10.07 |
| [수리통계학] 이산확률변수와 연속확률변수(Discrete and Continuous Random Variable) (2) | 2023.10.05 |
