[수리통계학] 확률변수의 기댓값(Expectation of Random Variable)

Review

참고 포스팅 :

2023.09.14 - [Statistics/Mathematical Statistics] - [수리통계학] 확률변수(Random Variable ; R.V.)

[수리통계학] 확률변수(Random Variable ; R.V.)

2023.10.05 - [Statistics/Mathematical Statistics] - [수리통계학] 이산확률변수와 연속확률변수(Discrete and Continuous Random Variable)

[수리통계학] 이산확률변수와 연속확률변수(Discrete and Continuous Random Variable)

# 해당 포스팅은 KOCW 김충락 교수님의 수리통계학 강의와 Hogg의 수리통계학개론(Introduction to Mathematical Statistics)를 기초로 작성되었습니다.

 

---

안녕하십니까, 간토끼입니다.

이번 포스팅에서는 확률변수의 중심 경향을 나타내는 지표로서 확률분포를 이해하는 데 도움을 주는 기댓값(Expected Value)에 대해 다뤄보겠습니다.

 
기댓값을 이해하기 위해 다음 예시를 살펴보겠습니다.

돌려돌려 돌림판 게임을 가정해봅시다. (보니하니? ㅎㅎ)
이 게임에 참여하기 위해서는 참가비 5달러($)를 지불해야만 합니다.
돌림판은 보시다시피 1부터 4까지 4개의 숫자 중 하나를 맞히는 방식으로 되어있고, 각 숫자에 따라 상금이 상이합니다.
 
돌림판 게임을 통해 나오는 숫자를 $X$라고 할 때 각 숫자에 따른 확률은 0.2, 0.3, 0.35, 0.15입니다.

그리고 상금은 숫자 4를 제외하고는 모두 5보다 작으므로, 이득(Gain) $G$을 상금에서 참가비를 뺀 값으로 정의하면 4를 맞혔을 때만 이득이고 나머지는 손해인 게임이네요.
다만 상대적으로 1,2,3 숫자에 대한 손해의 정도는 작아보이고, 4 숫자에 대한 이득의 정도는 크게 느껴집니다.
 
4를 맞혀서 한탕 챙기느냐, 아니면 손해를 보느냐 둘 중 하나의 결과를 얻는 게임이겠네요.
과연 이 게임을 참여하려는 참가자는 게임에 참가하는 것이 이득일까요, 참여하지 않는 것이 이득일까요?

단순히 상금만 놓고 보면 "참여해서 숫자 4를 맞히면 되는 거 아니야?" 라는 합리적인 기대가 충분히 들 수 있을 것 같습니다.
감에 의해 게임에 참여하는 것이 아니라 "확률적으로" 이 게임에 참여한다면 어느 정도의 수익을 거둘지 알려주는 지표가 있으면 좋을 것 같습니다.
 

이때 기댓값(Expectation of Random Variable)은 훌륭한 지표가 될 수 있습니다.
각 숫자에 따른 확률이 주어져있다고 가정했으므로, 기대 수익을 계산해보면 되죠.

각 숫자와 확률을 곱한 값을 다 더해주면 이 게임에 대한 기대 수익 $\sum G_{i} P_G(x_i)$이 됩니다.

계산해보면 기대수익은 -0.5달러네요. 게임에 참여하면 확률적으로 손해를 볼 가능성이 크므로, 합리적인 플레이어라면 굳이 사서 고생할 필요는 없을 것 같습니다.
 
이처럼 기댓값은 승산이 있는 게임에서 유래되었다고 합니다.
말 그대로 어떠한 확률 실험에 대해 기대하는 값(기댓값)이기 때문에, 어떠한 값이 나올지 예상할 수 있게 해주는 지표라고 이해해주시면 되겠습니다.
 

확률변수 X에 대한 기댓값은 위와 같이 정의할 수 있습니다.
위 예시에서 언급한 것처럼 확률변수 $X$가 가질 수 있는 모든 $x$에 각 확률 $p(x)$를 곱해서 더해주면 기댓값 $\sum x p_{X}(x)$ 됩니다.

만약 이산확률변수라면 sigma $\sum$ 를 이용해 합을 나타내고,
연속확률변수라면 integral $\int$ 을 이용해 합을 나타냅니다.
 
이때 조건을 보시면 $X$의 절대값 $\left|X \right|$의 기댓값에 대해 수렴한다는 조건, 즉 유한해야 한다는 조건이 붙습니다. 발산하면 기댓값을 정의할 수 없으니깐요.
이를 위해 합과 적분의 절대 수렴은 합과 적분의 수렴을 의미한다는 '절대 수렴'의 개념을 간단하게 짚고 넘어가겠습니다.

고마워요 챗GPT

이러한 이유때문에 기댓값을 정의할 때는 절대 수렴해야한다는 조건이 붙습니다.
이해가 되시죠?
 

728x90

 
이번에는 간단한 예시를 통해 기댓값을 이해해봅시다.

확률변수 $X$가 이산확률변수일 경우에는 앞선 케이스와 마찬가지로 구해주시면 됩니다.
그리고 연속확률변수라면 $S_x$에 대하여 적분을 해주시면 됩니다.
 
이쯤 되면 기댓값은 평균과 같은 것 같기도 하고, 다른 것 같기도 합니다.
앞서 돌림판 예시에서도 "확률적으로" 이 게임에 참여한다면 어느 정도의 수익을 얻을 수 있을지 예상할 수 있는 지표로서 기댓값을 언급했기 때문에, 우리가 일상에서 쓰는 평균과 같은 것 같단 생각이 드는데요.

이에 대한 답은 "같을 수도 있고, 다를 수도 있다." 입니다.
왜 그럴까요?

이는 정의하기 나름이어서 그렇습니다.
우리가 일상에서 사용하는 평균은 "산술평균"을 의미하기 때문이죠.

각 데이터를 다 더한 값 $\sum x_i$을 데이터의 총 개수인 $n$으로 나눠준 값으로 평균을 정의합니다.
그러므로 평균은 "각 데이터의 가중치가 $\frac{1}{n}$ 인 기댓값"과 같다고도 이해할 수 있을 것 같습니다.
 

하지만 각 확률변수에 대한 확률은 일반적으로 같지 않습니다.
그러므로 우리는 이러한 평균(기댓값)을 "가중평균(Weighted Average)"이라고 합니다.

즉 이론상으로 확률변수의 모든 값에 대한 확률이 모두 $\frac{1}{n}$으로 같다면 산술평균과 같겠지만 현실적으로는 어렵겠죠.

정리하자면 다음과 같습니다.
기댓값은 확률변수, 확률분포와 관련된 지표로서 확률변수의 중심 경향을 나타냅니다.
그리고 평균은 주어진 데이터의 대표값 정도로 이해하면 좋을 것 같습니다.
 

---

이번엔 지난 포스팅에서 다루었던 확률변환의 케이스를 생각해봅시다.

즉 기댓값을 갖는 확률변수 $X$가 존재한다고 할 때, 임의의 변환함수 $g$에 대하여 $Y = g(X)$를 만족하는 확률변수 $Y$를 가정합시다.

만약 이 $Y$의 기댓값을 구한다면 $Y$의 분포를 활용하면 쉽게 구할 수 있겠죠.
하지만 이게 현실적으로 어렵다면, 우리가 알고 있는 $X$의 분포를 이용해서 $Y$의 기댓값 $E(Y)$을 구할 수 있을까요?
 

네, 정답은 가능합니다.
마찬가지로 Y의 기댓값을 정의하기 전에 절대수렴을 가정할 수만 있다면, 위에서 보시는 것처럼 기댓값을 정의할 수 있습니다.

연속확률변수의 경우는 증명하기 까다롭기 때문에 이산확률변수의 경우를 증명해보겠습니다.

중간에 $\sum P_{X}(x) = P_{Y}(y)$ 은 주변확률분포를 알아야 이해할 수 있는 부분이지만, 저러한 관계가 있구나 정도로만 기억하시고 넘어가시면 될 것 같습니다.
 
연속확률변수의 경우는 직접 풀어보면서 이해해봅시다.

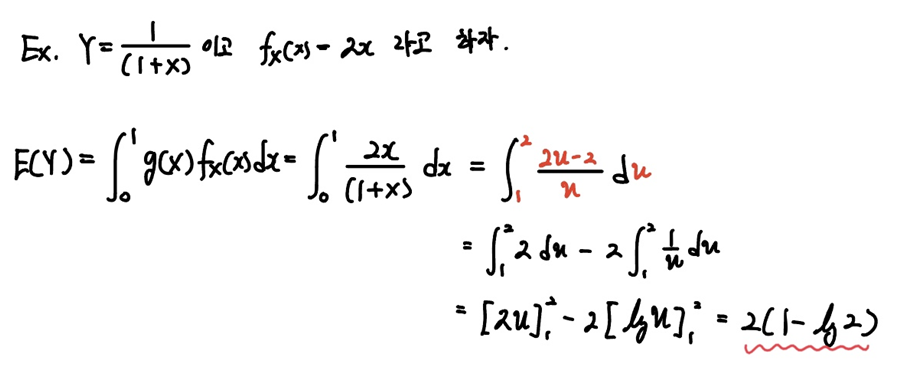
pdf로 $f(x) = 2x$를 갖는 확률변수 $X$가 존재할 때, $Y = g(x) = \frac{1}{1+x}$인 확률변수 $Y$를 가정합시다.
이때 $Y$의 기댓값은 $g(X)$와 $X$의 pdf인 $2x$를 활용해서 위와 같이 유도할 수 있습니다.
계산과정이 어렵진 않으니 넘어가겠습니다.
 

---

이번에는 또 다른 기댓값의 유용한 성질을 다뤄보겠습니다.
바로 기댓값의 선형성(Linear Property of Expectation)인데요.

 
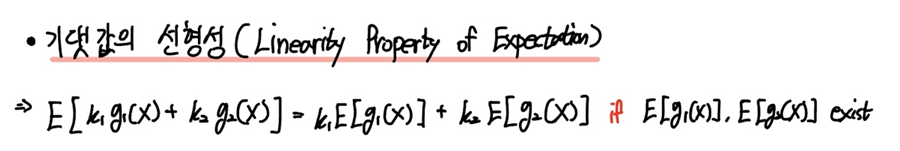
마찬가지로 확률변수 $X$가 존재하고, $g_{1}(X), g_{2}(X)$ 함수가 확률변수 $X$의 함수이며 이 함수들의 기댓값이 존재한다고 가정합시다.
이때 임의의 상수 $k_1, k_2$에 대하여 상수 $k$와 확률변수 $g(X)$의 선형결합의 기댓값이 존재하며, 이를 위와 같이 풀어서 나타낼 수 있습니다.

우리는 이를 "기댓값의 선형성(Linear Property of Expectation)" 이라고 합니다.
 
물론 확률변수의 각 형태에 따라서도 선형성이 유효함을 쉽게 보일 수 있습니다.

기댓값을 구성하는 $\sum$와 $\int$ 모두 선형 연산자임으로 선형성이 성립함을 쉽게 보일 수 있죠.
이를 통해 기댓값 연산자 $E$가 선형연산자임을 알 수 있습니다.

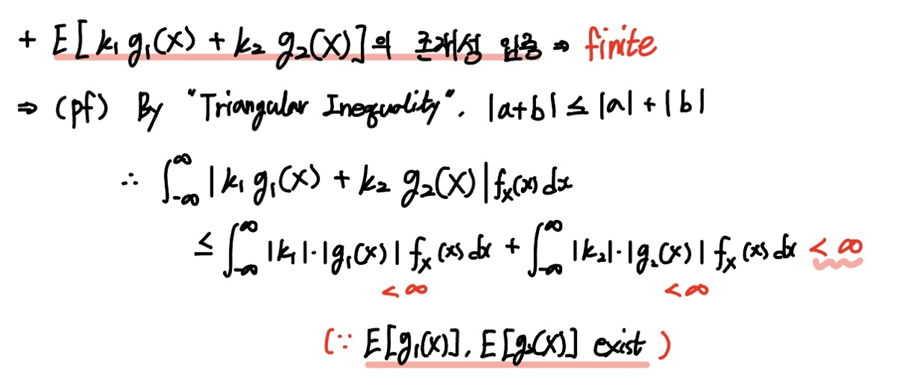
물론 $E[k_{1} g_{1}(X) + k_{2} g_{2}(X) ]$ 가 존재함을 보이기 위해서는 절대 수렴함을 보여야 하는데요.
이때 삼각부등식(Triangular Inequality)를 사용하면 쉽게 보일 수 있습니다.
 
삼각부등식은 실수의 합의 절대값은 각 실수의 절대갑의 합보다 작거나 같다는 것을 나타내는 부등식입니다.

즉 우변의 각 항이 유한함(finite)은 앞서 가정했기 때문에, 유한한 항끼리 더하면 유한함은 자명한 진술입니다.
그러므로 위 삼각부등식을 활용한 증명을 통해 기댓값이 유한함을 보일 수 있습니다.
 

다음 포스팅에서는 기댓값만큼 중요한 함수인 적률생성함수, 일명 mgf에 대해 다뤄보겠습니다.
 
감사합니다.
잘 읽으셨다면 게시글 하단에 ♡(좋아요) 눌러주시면 감사하겠습니다 :)
(구독이면 더욱 좋습니다 ^_^)

* 본 블로그는 학부생이 운영하는 블로그입니다.
따라서 포스팅에 학문적 오류가 있을 수 있으며, 이를 감안해서 봐주시면 감사하겠습니다.
 

---

- 간토끼(DataLabbit)
- B.A. in Economics, Data Science at University of Seoul