[수리통계학] 확률변수(Random Variable ; R.V.)
Review
# 해당 포스팅은 KOCW 김충락 교수님의 수리통계학 강의와 Hogg의 수리통계학개론(Introduction to Mathematical Statistics)를 기초로 작성되었습니다.
안녕하십니까, 간토끼입니다.
이번 포스팅에서는 확률변수(Random Variable; R.V.)에 대해 다뤄보겠습니다.

지난 포스팅에서는 확률실험, 그리고 확률실험의 모든 결과의 집합인 표본공간, 그리고 표본공간의 각 원소에 측도(measure)의 개념으로 확률을 부여하는 확률집합함수에 대해 다뤘습니다.
간단하게 확률실험의 예시를 들어보죠.

앞, 뒷면이 존재하는 동전을 던지는 실험을 가정합시다.
이때 앞면을 H, 뒷면을 T라고 하면 표본공간은 $C = {H, T}$ 라고 할 수 있습니다.
그리고 앞면이 나오면 1을 부여하고, 뒷면이 나오면 0을 부여한다고 합시다.
이는 다시 생각해보면 ${H, T}$를 정의역으로 하고, ${0, 1}$을 공역으로 하는 함수와 같은 얘기죠.
$X(T) = 0, X(H) = 1$ 이라고 할 수 있으니깐요.
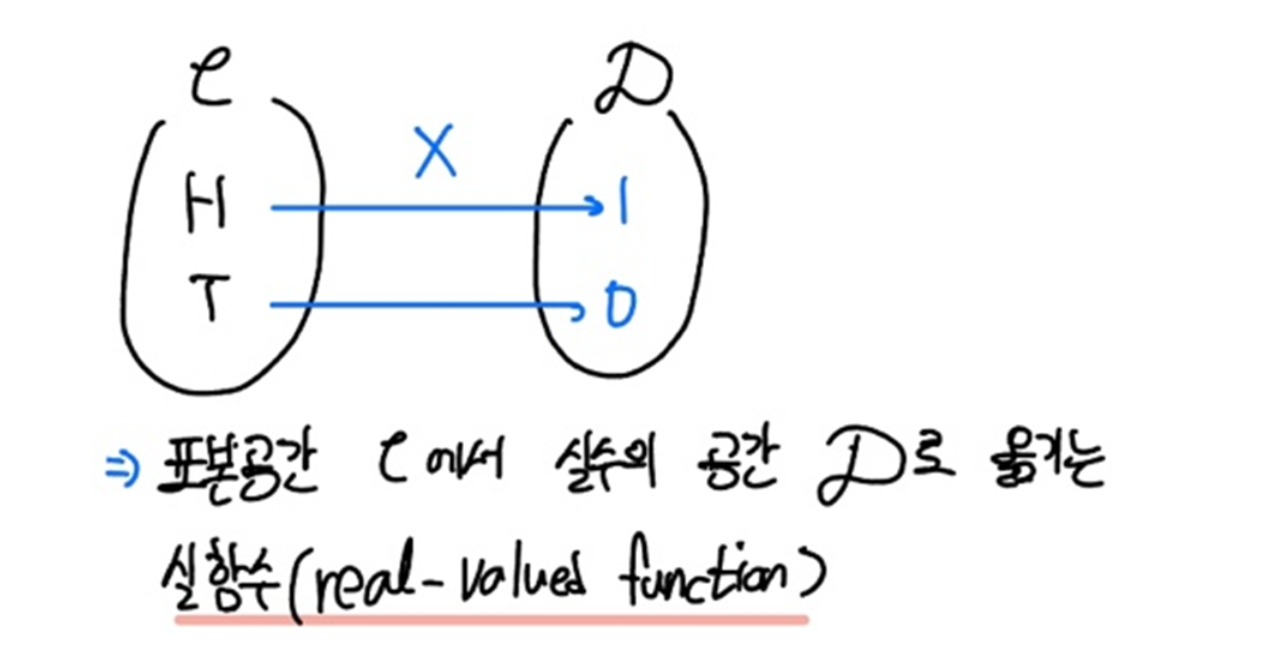
즉 이때의 함수 $X$는 표본공간에서 실수의 공간으로 옮기는 실함수(Real-valued Function)입니다.
이를 확률변수라고 합니다.

확률변수(Random Variable)는 표본공간에서의 각 원소 $c$에 오직 하나의 실수 $X(c) = x$를 대응시키는 함수를 의미합니다.
그리고 확률변수 X의 공간(space)을 $D_X$라고 하면, 공간 $D_X$ 는 $X(c) = x$ 를 만족하는 $x$ 의 집합임을 이해할 수 있으시겠죠.
이때 $D$ 가 Countable Set(가산형 집합)이라면 확률변수 $X$ 를 이산확률변수(Discrete R.V.)라고 하고,
Interval of Real Numbers(실수의 구간)이라면 연속확률변수(Continuous R.V.)라고 합니다.
이건 다음 포스팅에서 자세히 다루겠습니다.
위에서 소개한 개념을 도식화하면 다음과 같습니다.

표본공간 $C$ 와 확률변수 $X$ 의 공간인 $D_X$ 모두 sigma-field를 갖습니다.
그리고 sigma field가 정의됨에 따라 각각의 확률집합합수도 갖겠죠.
확률변수 X의 공간인 D에서 정의된 확률집합함수를 Induced Probability Function이라고 합니다.
이 확률함수는 확률변수가 이산형이냐, 연속형이냐에 따라 부르는 명칭이 상이합니다.
전자라면 확률질량함수(Probability Mass Function; PMF)라고 하고, 후자라면 확률밀도함수(Probability Density Function; PDF)라고 합니다.
이 개념도 이산확률변수와 연속확률변수를 다루면서 소개하겠습니다.
위에서 소개한 확률변수에 따른 확률함수(질량, 밀도)는 확률변수의 분포를 결정하는 함수입니다.
이번에 소개할 누적분포함수는 확률변수의 확률분포를 고유하게 결정하는 함수입니다.
1. 누적분포함수(Cumulative Distribution Function; CDF)

$X$ 가 확률변수일 때 누적분포함수(CDF) $F(x)$는 $-\infty$ 부터 $X = x$까지 합한 값,
즉 $F_{X}(x) = P(X \, \leq \, x)$로 정의됩니다.
예시를 살펴보죠.
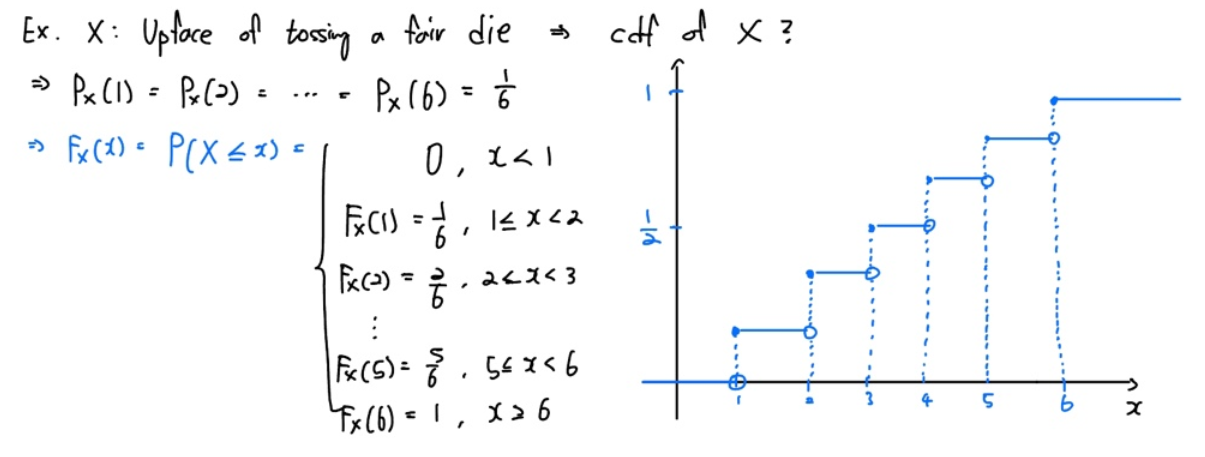
확률변수 $X$ 를 공정한 주사위(각 면의 확률이 동일할 때 fair라는 표현을 사용합니다.)를 던졌을 때 나오는 앞면의 숫자라고 합시다.
우리가 아는 주사위는 1부터 6까지의 눈으로 이루어진 정육면체이므로, 각 주사위의 눈이 나올 확률은 다음과 같겠죠.
$$ P(1) = P(2) = \cdots = P(6) = \frac{1}{6} $$
그렇다면 $X$ 의 공간인 $D_{X} = {1,2,3,4,5,6}$이 되므로, $X$ 의 CDF인 $P(X \, \leq \, x) $ 은 위와 같이 쉽게 구할 수 있습니다.
위 그림에서 우측에 있는 그래프를 살펴보면 몇 가지 눈에 띄는 성질이 있습니다.
먼저 $\infty$ 로의 극한값이 1이므로, 누적분포함수의 개념에 대입하면 모든 원소의 확률값을 다 더한 값은 1이 된다는 것이죠. 확률의 총합은 1이니까 이에 부합하는 성질입니다.
그리고 위 예시는 불연속점이 존재합니다. 비록 모든 구간에서 연속은 아니지만 불연속점에서 우극한(light-limit)과 함숫값이 같습니다.
또한 $-\infty$ 로의 극한값은 0이 되네요.
이러한 성질들을 정리하면 다음과 같습니다.
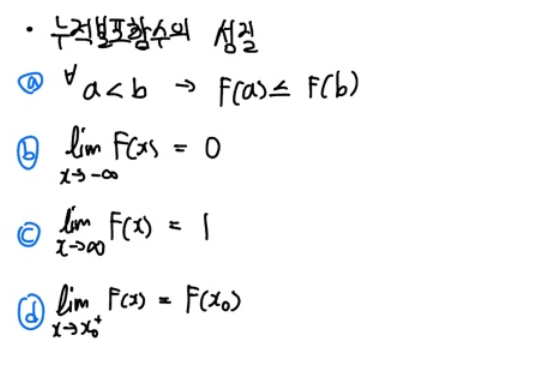
직관적으로 이해되는 성질들입니다. 어려울 건 없지만 4번째 성질은 헷갈릴 수 있습니다.
각 성질들을 하나씩 증명해보죠.
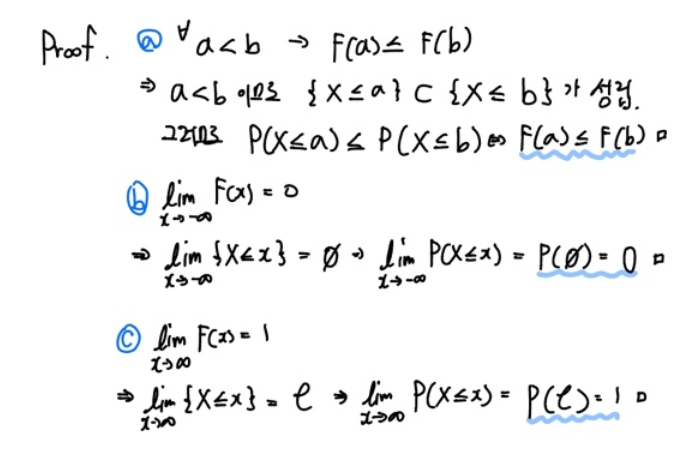
어렵지 않습니다. 직관적으로 이해되는 증명이라고 생각합니다.
1번째 성질은 CDF의 특성상 확률을 "누적"하여 더하기 때문에, 확률변수가 상대적으로 작은 값이라면 누적한 값도 같거나 작겠죠.
2번째 성질과 3번째 성질은 위에서 간단히 언급했고요.
조금 헷갈릴 수 있는 4번째 성질(d)만 따로 증명해보겠습니다.
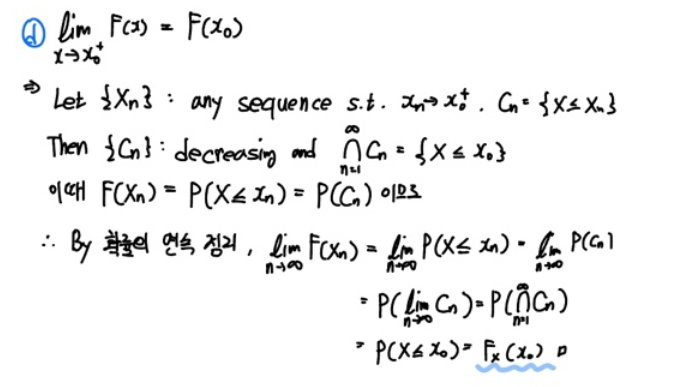
2023.07.21 - [Statistics/Mathematical Statistics] - [수리통계학] 불의 부등식(Boole's Inequality)
[수리통계학] 불의 부등식(Boole's Inequality)
Review 참고 포스팅 : # 해당 포스팅은 KOCW 김충락 교수님의 수리통계학 강의와 Hogg의 수리통계학개론(Introduction to Mathematical Statistics)를 기초로 작성되었습니다. 안녕하십니까, 간토끼입니다. 이번
datalabbit.tistory.com
위 증명을 이해하기 위해 이전 포스팅에서 '확률의 연속 정리'를 읽고 오시는 것을 추천합니다.
$x_0$의 우극한으로 수렴하는 임의의 배열 $x_{n}$, 그리고 $x_{n}$ 보다 작거나 같은 확률변수 $X$의 집합인 $C_n$ 을 가정합시다.
그러면 집합 $C_n$ 은 Decreasing Set이겠죠. $x_n$ 이 $x_0$ 으로 수렴할수록 $C_n$의 원소는 점점 줄어드니까요.
이때 $ F_{X}(x_n) = P(X \, \leq \, x_{n}) = P(C_{n})$ 이죠. 그러므로 다음과 같은 관계가 성립합니다.
$$ \lim_{n \to \infty} F(x_{n}) = \lim_{n \to \infty} P(X \, \leq \, x_{n}) = \lim_{n \to \infty} P(C_{n}) $$
여기서 확률의 연속 정리를 이용하면 limit와 확률 P를 바꿔도 성립하니까 $ \lim_{n \to \infty} P(C_{n}) = P(\lim_{n \to \infty} C_{n})$ 가 되겠죠.
그러면 다음과 같이 도출됨을 보일 수 있습니다.
$$ \lim_{n \to \infty}P(C_{n}) = P(\lim_{n \to \infty} C_{n}) = P( \bigcap_{n = 1}^{\infty} C_{n}) = P(X \,\leq\, x_{0}) = F_{X} (x_{0}) $$
직접 손으로 써보시는 것도 추천합니다.
즉 누적분포함수에서는 항상 함숫값과 우극한이 같습니다. 그러나 좌극한과 함숫값은 전 구간에서 항상 같지 않으므로 누적분포함수는 "항상 연속"인 함수는 아닙니다. (불연속점이 존재합니다.)
위 사실을 이용하면 다음과 같은 정리를 도출할 수 있습니다.

구간 (a, b] 의 확률값은 b까지의 누적분포함수에서 a까지의 누적분포함수를 뺀 값과 같습니다.
$$ P(a < X \, \leq b) = F_{x}(b) - F_{x}(a), \, \forall a < b $$
익숙한 notation이죠? 미적분의 기본정리입니다. 다음 포스팅에서 다루겠지만 확률밀도함수를 적분한 값은 누적분포함수가 됩니다.
그리고 P(X=x)는 누적분포함수의 함숫값에서 좌극한 값을 뺀 값이 됩니다. 다른 말로 하면 질량이 존재한다는 건데요.
$$ P(X = x) = F_{X}(x) - F_{X} (x^-) $$
만약 x가 누적분포함수의 불연속점이라면 확률값은 항상 0보다 큽니다. ($P(X = x) > 0$)
다음 포스팅에서는 앞서 언급한 이산확률변수와 연속확률변수에 대해 좀 더 다뤄보겠습니다.
감사합니다.
잘 읽으셨다면 게시글 하단에 ♡(좋아요) 눌러주시면 감사하겠습니다 :)
(구독이면 더욱 좋습니다 ^_^)
* 본 블로그는 학부생이 운영하는 블로그입니다.
따라서 포스팅에 학문적 오류가 있을 수 있으며, 이를 감안해서 봐주시면 감사하겠습니다.
- 간토끼(DataLabbit)
- B.A. in Economics, Data Science at University of Seoul