[회귀분석] 회귀계수의 유의성 검정

Review

참고 포스팅 : 

2022.03.03 - [Statistics/Regression Analysis] - [회귀분석] 가설검정의 기초 개념

[회귀분석] 가설검정의 기초 개념

2022.03.03 - [Statistics/Regression Analysis] - [회귀분석] 유의수준과 유의확률

[회귀분석] 유의수준과 유의확률

---

안녕하십니까, 간토끼입니다.

이번 포스팅에서는 이전 포스팅에서 다루었던 가설검정과 유의수준, 유의확률 등의 개념을 이용하여 회귀모형에서의 회귀계수에 대한 유의성 검정을 다뤄보겠습니다.

 

앞서 계속 다루었지만 회귀분석에서 회귀계수, 특히 기울기계수는 다음과 같은 의미를 가진다고 했습니다.

설명변수가 1개인 단순회귀모형에서 기울기계수 β_1의 부호에 따라 직선의 기울기가 달라진다고 하였죠.

 

하지만 만약 이 기울기계수가 0이라면 어떻게 될까요?

설명변수 X와 반응변수 Y 간에는 선형 관계가 없음을 알 수 있죠.

직관적으로 말하자면 두 변수 간 관련이 없다고도 할 수 있습니다. (엄밀히 말하자면 '선형 관계가 없다' 가 맞습니다. )

그러므로 기울기계수가 0일지 아닐지 살펴보기 위해 회귀계수의 유의성 검정이 필요한 겁니다.

 

지난 포스팅에서 다루었던 개념들을 이용하여 유의성 검정의 절차를 살펴보도록 하죠.

 

먼저 첫번째로 가설을 세워야 합니다.

귀무가설 H0 : β_1 = 0 이라고 할 수 있고, 대립가설은 이에 반대되는 0이 아니다라고 할 수 있죠.

이때 이 검정은 양측검정이 됩니다!

만약 단측검정을 하고 싶다면 대립가설을 0보다 크다, 혹은 0보다 작다로 설정하시면 됩니다.

 

두번째로는 귀무가설이 맞다 (H0 : β_1 = 0 이 참이다)라는 가정하에 검정통계량을 산출합니다.

단순회귀모형에서의 회귀계수의 분포는 자유도가 N-2인 t-분포를 따릅니다.

여담이지만 차후 다룰 설명변수가 K개인 다중회귀모형에서는 자유도가 N-K-1인 t-분포를 따릅니다.

 

아무튼 귀무가설에서 모수(Parameter)를 0으로 설정했으므로, 검정통계량 식에서 모수 β_1를 0으로 대입함으로써 식은 위처럼 단순하게 바뀝니다.

분모에 있는 s.e. 는 표준오차(Standard Error)입니다.

 

만약 회귀계수가 0인지를 검정하는 게 아닌, 1 혹은 다른 값임을 검정하고 싶다면 어떻게 될까요?

그러면 검정통계량 식에서 모수(Parameter)가 들어갈 자리에서 값만 바꿔주면 됩니다.

쉽죠?

 

그 다음은 유의수준을 결정해주면 됩니다.

통상 유의수준은 대개 5%로 설정하는데요.

다만 검정을 엄밀하게 하고 싶다면 유의수준을 0.001처럼 작게 할 수도 있고,

널널하게 하고 싶다면 0.1로 하면 됩니다.

유의수준이 작을수록 제1종오류를 그만큼 범하지 않으려고 한다는 것은 지난 포스팅을 통해 이해하셨을 거라 생각합니다.

 

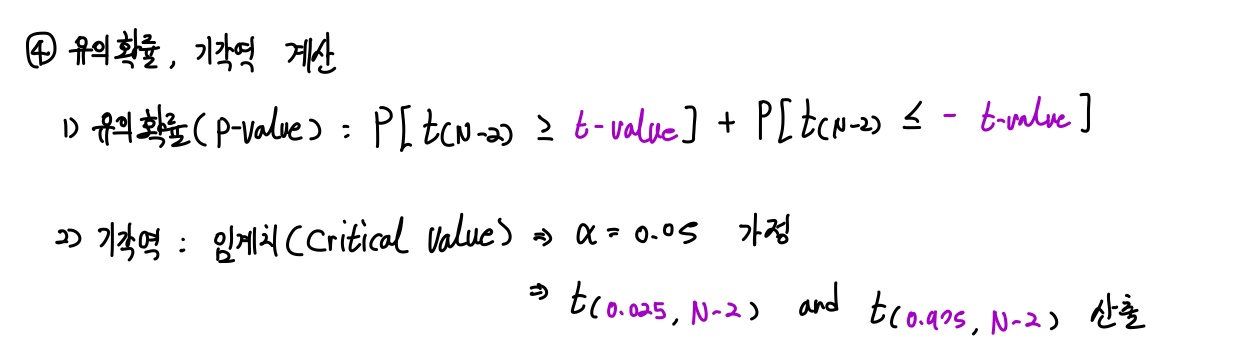
유의수준을 결정했으면 이에 따른 유의확률과 기각역(임계치의 값)을 결정해주면 됩니다.

유의확률은 확률분포함수에서 검정통계량이 차지하는 부분의 넓이값(확률값)으로 이해하면 됩니다.

임계치(Critical value)는 앞서 정한 유의수준와 자유도 하에서 t-분포표를 참고해 값을 정할 수 있는데요.

이후 예시를 통해 자세히 설명드리죠.

 

그래서 마지막은 앞서 구한 유의수준과 유의확률의 크기를 비교해 귀무가설의 기각 여부를 결정하시면 됩니다.

그리고 기각역에 검정통계량 값이 포함되는지 비교하기 위해서는 위와 같이 판단하시면 됩니다.

 

알기 쉽게 예시를 통해 살펴보죠!

 

 

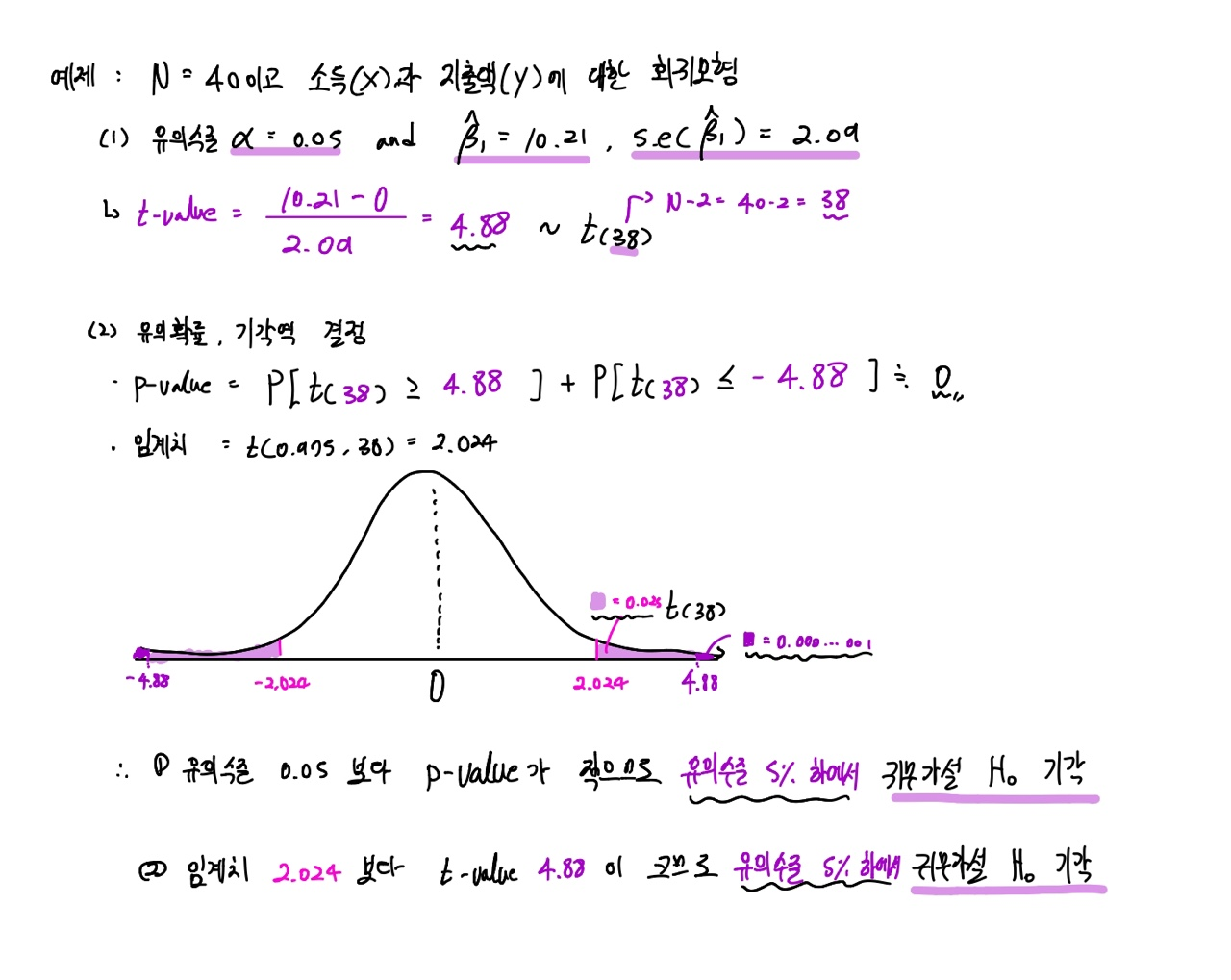
먼저 표본의 수(n)가 40이고, 소득(x)과 지출액(y)에 대한 회귀모형을 구축했다고 가정해보죠.

이때의 기울기계수가 0인지에 대한 가설검정 문제입니다.

먼저 유의수준은 0.05로 정했고, 최소제곱추정법을 통해 산출한 최소제곱추정량이 10.21이고, 표준오차는 2.09라고 가정할게요.

이때 검정통계량은 앞서 보여드린 식에 의거하여 4.88이라고 구할 수 있으며, 이 검정통계량은 자유도가 38인 t-분포를 따릅니다.

 

이어서 유의확률(p-value)과 임계치(critical value)를 구해보죠.

그전에 한번 T-분포표를 볼게요.

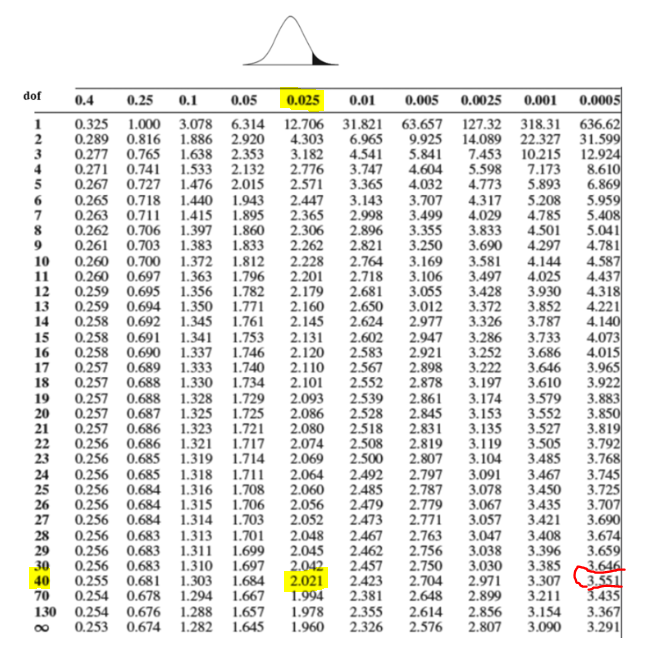
먼저 양측검정 문제이니까 우리가 설정한 유의수준 0.05는 양측검정이므로 이를 각 Side의 수인 2로 나눈 0.025가 되겠죠.

실제로 임계치 t(0.975, 38)의 값은 2.024이지만,

위 표를 참고해서 이에 근접한 자유도가 40일 때의 값을 찾아보면 2.021임을 알 수 있습니다.

 

그리고 검정통계량이 4.88일 때의 p-value도 위 표를 참고해 대략적으로 추측할 수 있어요.

검정통계량이 3.551일 때의 확률값은 0.0005가 되는데요.

그러니 검정통계량이 4.88이면 이것보다 훨씬 작은 0.000000000 .... 1 정도가 될테니, 거의 0이라고 봐도 되겠죠.

실제로는 컴퓨터 프로그램을 통해 산출해야 합니다. 값이 너무 작아서 손으로는 구하기 힘들거든요.

위 그림(확률밀도함수)을 보시면 대략적으로 어떤 느낌인지 이해하실 거라 생각합니다.

 

아무튼 기각역도 구했고, p-value도 구했으니 가설검정을 할 수 있겠죠.

(1) 유의수준 0.05보다 p-value = 0.00...01가 더 작으므로 유의수준 5% 하에서 귀무가설을 기각할 수 있다.따라서 회귀계수 β^_1은 유의수준 5% 하에서 통계적으로 유의하다.

 

(2) 임계치 2.024보다 검정통계량 t-value = 4.88이 더 크므로, 검정통계량은 기각역에 포함되어 유의수준 5% 하에서 귀무가설을 기각할 수 있다.따라서 회귀계수 β^_1은 유의수준 5% 하에서 통계적으로 유의하다.

 

이렇게 쓰시면 정답입니다!!

 

만약 프로그램으로 산출된 결과를 해석한다면 어떻게 하면 될까요?

예시로 R을 이용해 단순회귀분석을 한 결과를 해석해보죠.

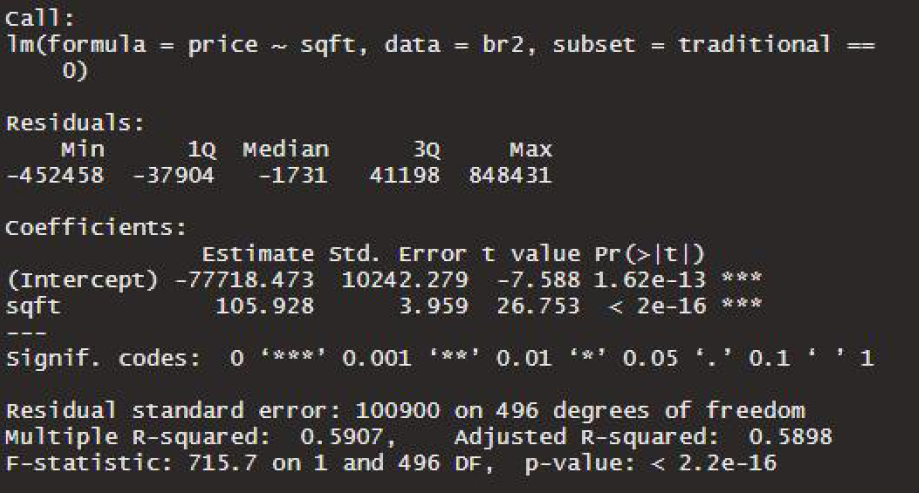
Intercept는 절편을 말하고, sqft는 설명변수입니다. (그냥 이 모형에서 설명변수의 변수명이 sqft 인겁니다.)

sqft의 회귀계수 추정치(Estimate)는 105.928이고, 표준오차(Std. Error)는 3.959이고, 이에 따른 t-value는 26.753이 되겠네요.

그리고 마지막은 p-value < 2e-16가 되겠습니다.

이때 2e-16의 의미는 소수점 16번째자리에 2가 있다는 의미입니다.

예시를 들면 1e-02 = 0.02, 3e-04 = 0.0003 이렇게 표기할 수 있어요.

따라서 유의수준이 5% (0.05)라고 가정할 때 p-value는 0.0000...002이므로 0.05보다 명백히 작습니다.

그러므로 유의수준 5% 하에서 귀무가설을 기각하므로, 위 회귀계수는 유의수준 5% 하에서 통계적으로 유의하다고 할 수 있습니다.

 

참고로 유의수준 n% 하에서 ~ 라는 말을 붙이는 게 굉장히 중요합니다.

왜냐하면 p-value가 0.058 이라고 가정하면, 유의수준 0.1 하에서는 통계적으로 유의하지만, 유의수준 0.05 하에서는 유의수준보다 p-value가 크므로 통계적으로 유의하지 않거든요.

즉 귀무가설의 기각 여부는 연구자가 설정한 유의수준에 따라 달라집니다!!!!

이 점을 명심하여서 가설검정을 적용하시기 바랍니다.

 

 

감사합니다.

잘 읽으셨다면 게시글 하단에 ♡(좋아요) 눌러주시면 감사하겠습니다 :)

(구독이면 더욱 좋습니다 ^_^)

 

 

 

---

 

- 간토끼(DataLabbit)

- University of Seoul

- Economics & Data Science