[회귀분석] 유의수준과 유의확률
Review
참고 포스팅 :
2022.03.03 - [Statistics/Regression Analysis] - [회귀분석] 가설검정의 기초 개념
[회귀분석] 가설검정의 기초 개념
안녕하십니까, 간토끼입니다. 이번 포스팅은 회귀분석을 위한 가설검정의 기초 개념을 소개하겠습니다. 사실 회귀분석을 접하기 위해서는 기초통계학이 당연히 전제가 되어야 하는데요. 다만
datalabbit.tistory.com
안녕하십니까, 간토끼입니다.
가설검정 시리즈의 2탄입니다.
지난 포스팅에 이어서 이번 포스팅에서는 유의수준과 유의확률을 알기 쉽게!! 설명하겠습니다.
*알기 쉬운 포스팅이 목적이므로, 예시 중 약간(?)의 통계적 오류가 존재할 수 있습니다. 양해바랍니다.

제1종 오류(Type 1 Error)
먼저 유의수준의 개념을 정의하기 전에 제1종 오류라는 개념을 정의하고 시작하겠습니다.

제1종 오류(Type 1 Error)란, 귀무가설이 참임에도 불구하고 기각하는 오류를 말합니다.
즉, 기존 주장이 참이었음에도 불구하고 이를 기각하고, 실수로 대립가설을 채택하는 것이죠.
만약 대한민국 성인 남성의 평균키가 165cm라는 주장이 팩트였음에도 불구하고,
우리가 임의로 추출한 표본 성인 남성 100명의 키의 평균을 구해봤더니 165cm가 아니길래 냅다 귀무가설을 기각해버린다면 이는 제1종 오류에 해당합니다.
그러므로, 우리는 이러한 실수를 겪지 않도록 엄밀하게 분석할 필요가 있습니다.
유의수준(Level of Significance)

그래서 우리는 유의수준(Level of Significance)이라는 개념을 도입합니다.
제1종 오류의 최대 허용 한계를 설정하는 것인데요. 쉽게 말해서 실수할 확률의 마지노선을 의미합니다.
이게 어떤 의미냐?
비유를 하자면 이런 거죠.
성인 남성의 평균 키를 검정하기 위해 임의로 100명을 추출해서 구한 키가 172cm라고 가정합시다.
실제로 대한민국의 성인 남성들의 키가 대부분 커서 평균키가 165cm보다 크다면 모르겠지만, 유독 이번 표본이 키가 큰 사람들이 많이 뽑혀서 운좋게(?) 표본평균이 크게 나왔을 가능성도 있겠죠.
만약 이번 표본만 172cm로 표본평균이 산출되고, 다음 표본, 그 다음 표본의 표본평균을 산출했을 땐 165cm와 근접한다면 첫 번째 표본만으로 귀무가설을 기각하기에는 섣부른 선택일 수 있습니다.
그래서 우리는 이 운빨겜에 운명을 맡기기 보다는 안전장치를 마련해놔야 합니다.
그 안전장치가 유의수준이라고 생각하시면 이해하기 편할 거라고 생각합니다.
이 유의수준은 얼마나 엄밀하게 가설을 검정하냐에 따라 크기를 다르게 설정할 수 있습니다.
유의수준 α는 통상 0.1, 0.05, 0.01 등으로 설정하는데요. (유의수준은 확률값입니다.)
α가 클수록 오류를 허용하는 기준이 커진다는 의미겠죠? 보다 널널하게 검정함을 의미합니다.
반대로 α가 작을수록 (0.01) 오류를 최대한 허용하지 않는다는 것이니, 엄격하게 검정함을 의미합니다.
기각역

기각역은 귀무가설의 기각으로 이어지는 검정통계량의 범위를 의미한다고 지난 포스팅에서 설명하였습니다.
이를 위 유의수준과 엮어서 설명하면, 유의수준 α는 기각역의 크기를 결정하는 데 영향을 줍니다.
기본적으로 유의수준, 나아가 제1종 오류는 발생하기 어렵다는 가정 하에서 출발하는데요.
(발생하기 쉽다면 검정 자체가 곤란할테니깐요.)
기각역은 기본적으로 귀무가설이 참인 경우 발생하기 어렵거나 발생할 확률이 낮은 값으로 구성됩니다.
이는 검정통계량 값이 발생할 확률이 낮은 영역(유의수준)에 속하는 경우, 검정통계량은 가정된 분포를 갖기 어려우며 이에 따라 귀무가설이 참이기도 어렵다는 의미입니다,
사실 검정 통계량의 식에서 '귀무가설이 참이다'를 전제로 하는 부분이 있기 때문에 이런 해설이 나오는 건데 ... 좀 헷갈리는 부분입니다.
좀 더 이어서 설명해보면 이해가 되실 겁니다.
유의확률(p-value)

유의확률, 다른 말로 p-value라고도 부릅니다.
이는 귀무가설을 가정했을 때 주어진 자료가 발생할 확률을 의미합니다.
주어진 자료라고 하면 우리가 갖고있는 표본을 말하겠죠?
그리고 이 표본을 바탕으로 우리가 세운 가설(대립가설)이 맞는지, 틀린지 검정을 할 겁니다.
그래서 유의확률은 우리가 뽑은 표본의 데이터들이 대립가설에 힘을 실어주게 될 확률이라고 말할 수 있습니다.
이게 무슨 소리냐?
만약 대한민국 성인남성 평균 키가 165cm라는 게 참(True)이라고 가정할게요.
이때 우리가 가진 샘플로부터 얻어낸 표본평균이 172cm라고 가정하면,
평균키 165cm가 참인데, 표본평균키가 172cm 나올 수가 있어???? 에 대한 확률이 유의확률인 겁니다.
그러므로 유의확률은 작을수록 우리의 주장에 힘을 실을 수 있습니다.
기존 주장이 참이 아니라는 것이죠.
만약 유의확률이 크다면 관측값이 귀무가설 하에서 흔히 나올 수 있는 값이라는 것이므로, 귀무가설을 기각할 근거가 되지 않는다고 할 수 있습니다.

위와 같은 예시를 가정할게요.
검정통계량이 표준정규분포를 따르고, 표본으로부터 구한 검정통계량 값이 2라고 합시다.
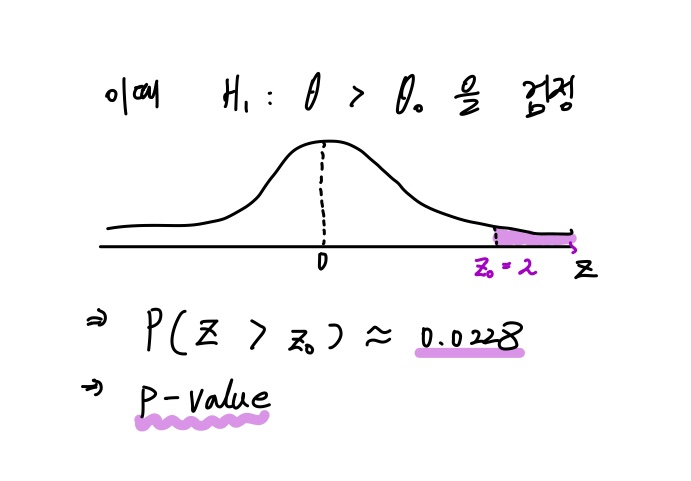
유의확률 p-value는 유의수준과 동일하게 확률입니다.
그러므로 확률밀도함수에서의 넓이(적분값)에 해당하며, P(Z>z0)에 해당하는 확률값이 되겠습니다.
개념을 종합적으로 아래 예시를 통해 정리해보죠.

A학교의 3학년 학생들의 평균 성적이 70점이라고 가정하겠습니다.
이때 어떤 선생님이 "우리 학생들이 그렇게 공부를 못할리가 없어!!!!" 라며 70점보다는 높을 거라고 생각합니다.
그래서 실제로 검증하기 위해 무작위로 50명을 선정(Sample)해서 평균 점수를 산출합니다.
(전교생이 많았나봐요... 사실 전교생 성적 구해보면 되지만 예시니까 ...)
이때 선생님께서는 71점, 72점 정도로는 표본을 잘 선정하는 등 운의 영향이 있을 수 있으니 최소 73점보다는 높아야 이 표본평균 점수를 신뢰하겠다고 생각했습니다.
그래서 표본평균을 구해봤더니 75점이 나왔고, 운빨의 기준인 73점보다 높으니 평균이 70점이라는 기존 주장을 기각합니다.

이를 가설검정의 요소에 대입하면 위와 같습니다.
유의수준을 저렇게 특정 점수로 한정하지는 않습니다!! 예시를 든 것입니다.
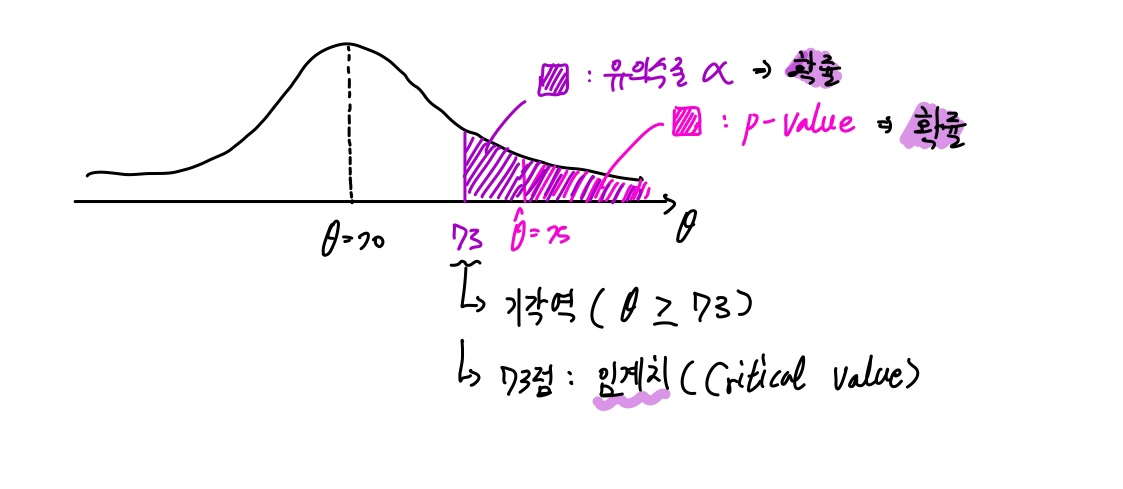
확률밀도함수 하의 각 요소를 도식해보았습니다.
위 문제를 예시로 들면, 73점은 임계치(Critical value)라고 합니다. 기각으로 가냐, 안 가냐의 경계선 정도로 이해하시죠.
그리고 임계치보다 큰 영역을 기각역이라 할 수 있습니다.
나아가 기각역이 해당하는 부분의 넓이(확률)를 유의수준이라고 부를 수 있고요.
우리가 구한 검정통계량으로부터 확률밀도함수의 넓이를 유의확률(p-value)이라고 부를 수 있습니다.
오! 여기서 흥미로운 사실을 알 수 있네요.
검정통계량과 기각역(임계치)는 X축 상의 값을 의미한다는 것이고,
유의수준 α와 유의확률 p-value는 확률, 즉 넓이를 의미한다는 것이죠.
그러니까 귀무가설을 기각하는지의 여부를 따질 때 두 가지 측면으로 따져볼 수 있다는 거예요.
(1) 검정통계량이 기각역에 포함된다면 (즉, 임계치보다 크다면)
(2) 유의수준의 크기보다 유의확률이 작다면
귀무가설을 기각할 수 있겠네요.
이제 이 가설검정의 개념들이 이해가 되시나요?
다음 포스팅에서는 지금까지의 개념들을 이용하여 실제로 회귀계수가 통계적으로 유의한지 따지기 위해 예시 문제를 통해 살펴보도록 하겠습니다
.
감사합니다.
잘 읽으셨다면 게시글 하단에 ♡(좋아요) 눌러주시면 감사하겠습니다 :)
(구독이면 더욱 좋습니다 ^_^)
- 간토끼(DataLabbit)
- University of Seoul
- Economics & Data Science