Review
참고 포스팅 : 2020/05/18 - [Statistics/Basic Statistics] - [기초통계학] 확률변수와 기댓값, 분산
[기초통계학] 확률변수와 기댓값, 분산
Review 참고 포스팅 : 2020/05/15 - [Statistics/Basic Statistics] - [기초통계학] 기술통계학(Descriptive Statistics)기초 2 - 모집단과 표본집단 with 모수&통계량 [기초통계학] 기술통계학(Descriptive Stati..
datalabbit.tistory.com
안녕하십니까, 간토끼입니다.
지난 포스팅에서는 확률변수에 대해서 정의하고, 이를 이용하여 기댓값과 분산에 대해서 다뤄봤습니다.
이번 포스팅에서는 공분산과 상관계수라는 중요한 개념에 대해서 다뤄보도록 하겠습니다.
실제로 데이터 분석을 하다 보면, 분석에 바탕이 되는 중요한 분석 기법 중 하나가 상관분석입니다.
내가 가진 데이터의 변수들 간의 서로 어떠한 관계가 있는지 살펴보는 것인데요.
예를 들어 특정 식료품 마트의 매출 데이터를 분석해보니,
X = 우유 판매량 , Y = 빵 판매량 이라는 데이터에서 서로 양의 관계가 있음을 확인하였다고 가정합시다.
빵을 사는 사람이 우유도 같이 산다, 또는 그 역의 관계는 우리의 직관과 부합하는 진술이기는 하죠?
다만 단순히 관계가 있다 와 얼마만큼의 관계가 있다는 누군가를 설득시키는 데 있어 큰 차이를 보일 것입니다.
왜냐하면 정성적인 진술보다도, 수치에 의거한 정량적인 진술이 누군가에게 신뢰를 줄 수 있기 때문이죠.
이번 포스팅에서는 이 수치에 의거한 얼마만큼의 관계가 있다~에 대해서 다뤄보도록 하겠습니다.

1. 공분산(Covariance)
먼저 공분산입니다.
공분산은 임의의 두 확률변수 X, Y 사이의 선형관계에 대한 정보를 알려주는 sign이라고 생각하시면 됩니다.
즉 공분산이 양수라면, 두 확률변수는 서로 양의 선형(linear) 관계가 있음을 의미하고,
공분산이 음수라면, 두 확률변수는 서로 음의 선형(linear) 관계가 있음을 의미합니다.
단 공분산은 두 변수의 scale에 따라 값이 크게 달라지므로, 단순히 공분산이 더 크다고 해서 선형관계가 강한 것은 아닙니다.
예를 들어 X, Y의 공분산이 14 이고, W,V의 공분산이 100이라면
두 조합 모두 양의 상관관계가 있음은 자명하지만, (X,Y)의 관계보다 (W,V)의 관계가 더욱 상관 정도가 크다라는 진술은 틀렸다는 겁니다.
이러한 오판을 방지하기 위해, 이후 다룰 상관계수를 이용합니다.
공분산의 공식은 지난번 분산의 공식 유도과정처럼, 약간의 유도과정을 통해 쉽게 바꿀 수 있습니다.

중간에 보면 '상수는 기댓값(Expectation) 밖으로 나올 수 있다< E(aX) = aE(X)> 는 성질을 이용했습니다.
뭐 어려울 거 없이 쉽죠?
그럼 한번 위 공식을 이용하여 직접 공분산을 구하기 위해 예시를 들어보겠습니다.
음... 한번 5명의 학생의 키(X)와 몸무게(Y)의 자료가 있다고 가정해봅시다.
| 이름 | A | B | C | D | E |
| 키(X) | 170 | 180 | 158 | 163 | 185 |
| 몸무게(Y) | 60 | 70 | 52 | 59 | 92 |
먼저 우리의 직관과 부합하는 진술은 키가 클수록 몸무게도 클 것이다 or 몸이 많이 무거울수록 키도 클 것이다 겠죠?
부합하는지 한번 공분산을 이용해 검증해봅시다.

공분산이 128.68이 나오네요.
공분산이 양수니까 양의 상관관계가 있다고 이해해도 되겠죠? 우리의 직관과 부합하는 결과가 나왔습니다.
공분산도 기댓값과 분산과 마찬가지로, 몇가지 성질이 있는데요.
역시 네이버 백과사전의 힘을 빌렸습니다.
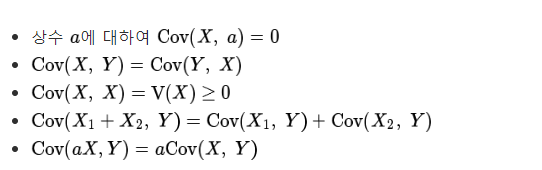
이때 분산과 공분산의 관계를 나타내는 중요한(?) 부등식이 있는데요.
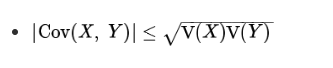
이것도 간단한 증명을 통해 부등식을 유도해보겠습니다.

잘 풀었는진 모르겠는데 그냥 참고용으로... 만약 틀렸다면 댓글 남겨주세요.
이때 분산의 성질인
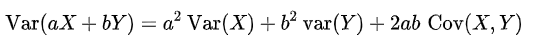
를 이용했습니다.
그리고 독립이라는 개념은 나중에 다루려고 했는데, 마침 나왔으니...
두 확률변수 X, Y가 독립이면 X,Y의 공분산 Cov(X, Y)는 0입니다.
공분산이 0이라는 의미는, 두 변수간 아무런 선형 상관관계가 없다는 것이죠.
그러나 역의 진술인 X,Y의 공분산 Cov(X,Y) = 0이면 두 확률변수 X,Y는 독립이다는 참이 아닙니다.
간단한 증명과정입니다.

참고로 두 변수가 독립이면, P(A)P(B) = P(A, B) 가 성립합니다.
2. 상관계수(Coefficient of Correlation)
그럼 이번에는 상관계수에 대해서 다뤄보겠습니다.
위에서 공분산의 크기는 상관관계의 절대적인 크기 자체를 의미하는 것이 아니다라고 했죠.
이는 공분산이 두 확률변수의 scale에 크게 영향을 받기 때문입니다.
그렇기에 상관 정도의 절대적인 크기를 측정할 수 있도록 해주는 것이 바로 상관계수입니다.
공식은 위에 나온 것처럼 공분산에 두 변수의 표준편차로 나눠주면 됩니다.
즉, 각 변수의 표준편차로 나눠주므로 어떤 scale이든 같은 값을 얻게 됩니다.
상관계수는 위 분산과 공분산의 관계를 나타내는 부등식을 이용하여,
-1부터 1사이의 값을 가지는데요.
1에 가까울수록 두 확률변수가 양의 선형 상관관계를 갖는다고 하고,
-1에 가까울수록 두 확률변수가 음의 선형 상관관계를 갖는다고 합니다.
그리고 만약 상관계수가 0이면 두 확률변수는 아무런 선형 상관관계를 갖지 않는다고 합니다.
핵심은 선형(linear)이라는 것에 있습니다.
위 키, 몸무게 예제를 통해 상관계수를 구해봅시다.

참고로 저 상관계수 기호는 로(rho)라고 발음합니다. 콩나물같죠?
이제 우리가 갖고 있는 데이터의 상관 정도는 0.73 이라고 자신있게 외칠 수 있습니다.
한번 plot으로 그려볼까요? 사실 관측치가 저렇게 적은 경우는 일반화하기 어렵지만..
선형의 의미가 갖는 모습을 한번 봅시다.
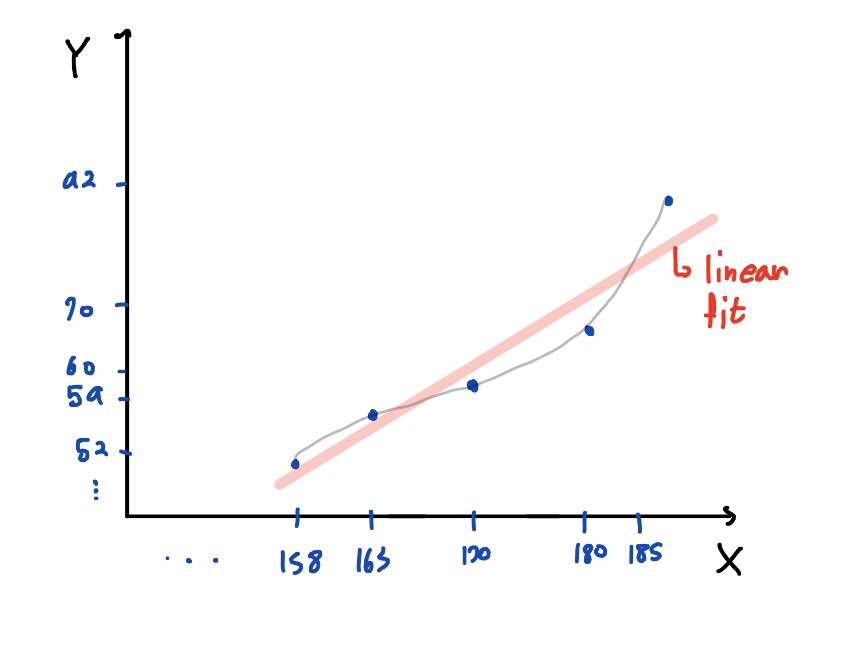
실제로 관측치 간 그래프를 그려보면 완벽히 선형이라고 보긴 어렵지만,
상관계수는 선형의 관계 정도만을 측정하므로, 대충 저런 빨간 직선을 긋는다고 생각하시면 됩니다.
(저 빨간 직선은 이후 회귀분석 파트를 다룰 때 다시 나올 예정입니다)
즉, 내가 가진 데이터가 비선형이라면 사실 상관계수는 적절한 지표가 아닐 수 있어요.
또한 이상치(Outliers)에 영향을 받으므로, 계수값이 왜곡될 수 있다는 단점이 있습니다.
오늘은 공분산과 상관계수에 대해서 다뤄봤습니다.
다음은 뭘 다뤄보지... 아 확률을 좀 더 다뤄봐야겠네요.
확률 중 조건부확률과 이를 이용한 베이즈정리에 대해서 다뤄보겠습니다.
감사합니다.
잘 읽으셨다면 게시글 하단에 ♡(좋아요) 눌러주시면 감사하겠습니다 :)
(구독이면 더욱 좋습니다 ^_^)
- 간토끼(DataLabbit)
- University of Seoul
- Economics, Big Data Analytics
'Statistics > Basic Statistics' 카테고리의 다른 글
| [기초통계학] 확률(Probability) 2 - 결합확률, 주변확률, 조건부확률 (6) | 2020.05.21 |
|---|---|
| [기초통계학] 확률(Probability) 1 - 확률의 기본 개념 (0) | 2020.05.20 |
| [기초통계학] 확률변수와 기댓값, 분산 (2) | 2020.05.18 |
| [기초통계학] 기술통계학(Descriptive Statistics)기초 2 - 모집단과 표본집단 with 모수&통계량 (2) | 2020.05.15 |
| [기초통계학] 기술통계학(Descriptive Statistics)기초 1 - 평균, 분산, 표준편차 등 (6) | 2020.05.14 |
