[회귀분석] 가우스-마르코프 정리(Gauss-Markov Theorem) 증명

Review

참고 포스팅 : 

2020/10/10 - [Statistics/Regression Analysis] - [회귀분석] 최소제곱추정량 β1를 선형 추정량으로 유도하기

[회귀분석] 최소제곱추정량 β1를 선형 추정량으로 유도하기

2020/10/13 - [Statistics/Regression Analysis] - [회귀분석] 최소제곱추정량 β1의 기댓값, 분산 유도

[회귀분석] 최소제곱추정량 β1의 기댓값, 분산 유도

---

안녕하십니까, 간토끼입니다.

 

지난 포스팅에서 최소제곱추정량을 선형 추정량으로 표현하고, 이를 이용해 기댓값과 분산을 유도했었죠.

이번 포스팅에서는 단순회귀분석의 가정을 만족할 경우 우리가 구한 최소제곱추정량이 BLUE(Best Linear Unbiased Estimator)라는 것을 보이는 가우스-마르코프 정리(Gauss-Markov Theorem)을 증명해보이겠습니다.

 

 

 

---

가우스-마르코프 정리는 다른 말로 가우스-마코프 정리라고도 합니다.

마르코프라는 학자를 읽는 방법이 조금씩 달라서 그런 것 같아요.

편한대로 생각하시면 됩니다.

 

각설하고 가우스-마르코프 정리를 보이기 위해서는 먼저 회귀모형이 회귀분석의 기본 가정을 만족한다고 가정해야 합니다.

(가정을 만족한다고 가정? ㅎㅎ)

 

 

 

다시 한번 살펴보면 이와 같습니다.

이전에 한번 다뤘었는데요. => 링크(단순회귀분석의 개념)

그래서 굳이 설명은 안하고 넘어가겠습니다.

 

 

 

가우스-마르코프 정리는 이러한 회귀분석의 가정이 성립할 때 최소제곱추정량이 가장 작은 분산을 갖는 효율적인 추정량임을 말하는 것입니다.

BLUE(Best Linear Unbiased Estimator)라는 말처럼 선형 불편추정량 중 제일 최고(Best)라는 거죠.

 

 

 

 

이를 보이기 위해 OLS추정량 β^이 아닌 다른 선형불편추정량 β*가 있다고 가정하겠습니다.

이 β*는 β^와 유사하게 y의 가중평균꼴로 표현되며, 이때의 ki 또한 임의의 상수라고 가정합니다.

 

즉, 임의의 상수이므로 ki는 기존 wi에 ci라는 또 다른 상수를 더한 꼴로 표현을 해도 무리는 없겠죠.

 

그렇다면 β*은 다음과 같이 나타낼 수 있습니다.

 

 

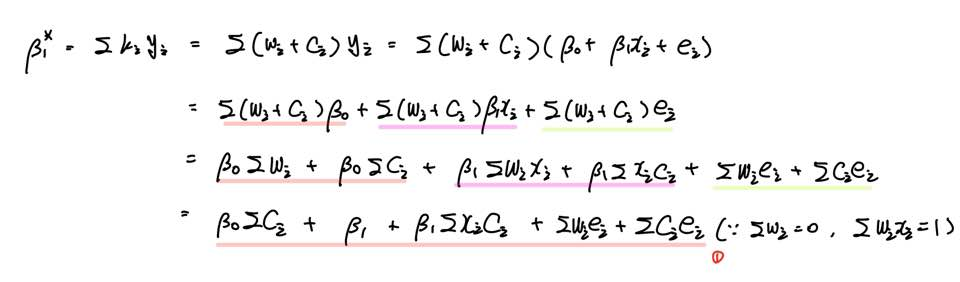
이때 앞선 포스팅에서 다루었던 w의 성질을 이용합니다. (못 보신 분들은 이전 포스팅을 참고해주세요.)

그러면 β*은 (1)번과 같은 식이 됩니다.

 

 

 

이때 우리가 위에서 가정하고 넘어간 게 있습니다.

 바로 β*은  β의 또 다른 선형불편추정량 중 하나라는 거였죠.

그렇기에 불편성을 만족하므로, β*의 기댓값은  β이 됩니다.

 

 

 

따라서 (1)식에 기댓값을 취해주면 β가 돼야 하기 때문에,

∑ci = 0, ∑xici = 0 이 돼야 함을 자연스럽게 유도할 수 있습니다.

 

 

 

 

위에서 유도한 ∑ci = 0, ∑xici = 0 을 바탕으로 β*을 다시 정의하면 위와 같습니다.

핵심은 β* 또한 OLS 추정량 β^과 마찬가지로 모수 β에 오차항이 더해진 꼴로 나타낼 수 있다는 것이죠.

 

 

 

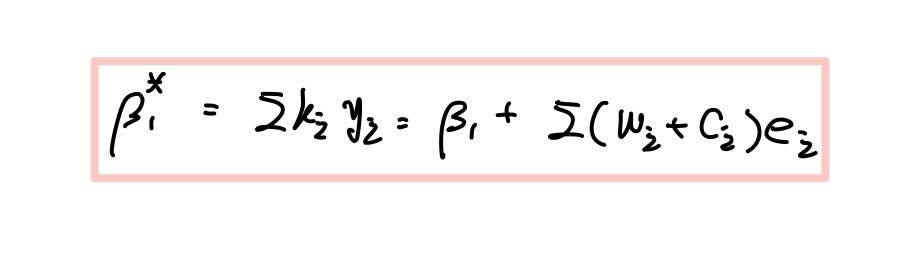
다시 쓰면 이와 같습니다.

 

 

이제  β*와 β^의 분산을 비교하여 누구의 분산이 더 작은지 비교해봅시다.

우리는 임의의 모수(Parameter)에 대한 여러 추정량 중 분산이 더 작은 추정량을 효율적인 추정량이라고 불렀습니다.

그래서 둘 중 어느 추정량이 더 효율적인 추정량인지 보이면 되는 것입니다.

 

 

 

 

따라서 OLS추정량이 아닌 다른 선형 불편추정량 β*들은 최소제곱 추정량 β^의 분산보다 더 크거나 같은 분산을 갖는다고 할 수 있습니다.

 

만약 β*에서 상수항 ci가 모든 i에 대해 0이라면 두 추정량의 분산은 같아지겠죠.

이 경우 β* = β^ 가 됩니다.

 

따라서 OLS추정량 β^보다 나은 β의 다른 선형불편추정량은 존재하지 않으며 이로써 가우스-마르코프 정리를 증명하였습니다.

 

감사합니다.

잘 읽으셨다면 게시글 하단에 ♡(좋아요) 눌러주시면 감사하겠습니다 :)

(구독이면 더욱 좋습니다 ^_^)

 

 

 

---

- 간토끼(DataLabbit)

- University of Seoul

- Economics, Big Data Analytics