[회귀분석] 최소제곱추정량 β1의 기댓값, 분산 유도

Review

참고 포스팅 : 

2020/10/10 - [Statistics/Regression Analysis] - [회귀분석] 최소제곱추정량 β1를 선형 추정량으로 유도하기

[회귀분석] 최소제곱추정량 β1를 선형 추정량으로 유도하기

---

안녕하십니까, 간토끼입니다.

 

지난 포스팅에서 β1의 최소제곱추정량을 선형 추정량 형태로 유도해보았습니다.

이번 포스팅에서는 이 선형 추정량 형태를 이용해  단순회귀분석의 고전적 가정을 바탕으로 β1의 기댓값과 분산을 유도해보겠습니다.

 

---

 

먼저 간단하게 다시 복습해보죠.

β1의 추정량은 다음과 같이 나타낼 수 있었습니다.

 

이를 이전 포스팅에서 선형 추정량의 형태로 다시 나타내었죠.

최종적으로 추정량은 모수(Parameter)와 가중치 wi, 오차 e에 대한 꼴로 나타낼 수 있었습니다.

즉 표본으로부터 얻어낸 추정량은 실제 참값과 ∑wiei 만큼 차이가 있다는 것이죠.

 

다만 오차와 실제 참값인 모수는 우리가 관측할 수 없기에 위 식은 이론적으로만 살펴보기 용이합니다.

즉 실제로 위 식을 계산하여 추정량을 얻어내기엔 어렵다는 것이죠.

 

그래서 실제로는 위 식은 추정량의 특성을 바탕으로 기댓값, 분산을 얻어내기에 용이한 '이론적인 식' 정도로만 생각하시면 좋습니다.

 

 

1. β1의 추정량의 기댓값 유도

먼저 β1의 추정량은 표본이 수집될 때까지 그 값을 알 수 없으므로 확률변수(Random Variable)입니다.

그리고 단순회귀모형에 대한 가정이 준수될 경우, β1의 추정량의 기댓값이 β1과 동일해지는지를 살펴보고자 합니다.

 

만약 추정량의 기댓값이 모수와 동일해진다면, 우리는 이러한 추정량을 불편추정량(Unbiased Estimator)라고 합니다.

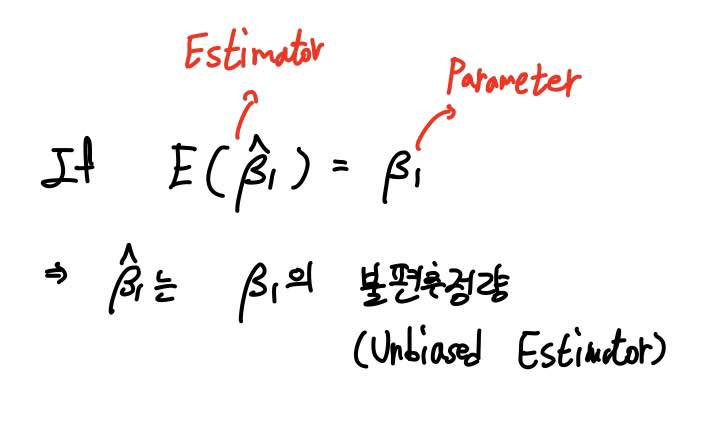
불편성에 대해서 간단하게 언급하자면, 충분히 큰 N에 대하여 크기가 N인 표본이 충분히 많이 수집되어 각 표본에 대해 β1의 추정량을 구하면, 이 추정량의 평균은 모수 β1이 된다는 것입니다.

자 그럼 위 식에서 확률적인 성분과 확률적이지 않은 성분을 구분해보죠.

먼저 모수는 모집단으로부터 얻어낸 회귀모형의 회귀계수니까 정해져있는 값이죠?

확률적이지 않으므로 확률변수가 아닌 상수라고 간주합니다.

 

그리고 wi도 확률적이지 않은 xi로부터 얻어낸 요소이기에 확률적이지 않습니다.

따라서 오차항만 유일하게 확률적인 요소겠네요.

 

이를 바탕으로 기댓값을 다음과 같이 보일 수 있습니다.

어렵지 않죠?

오차항의 기댓값은 0이 된다는 단순회귀분석의 가정을 이용해주었습니다.

 

 

2. β1의 추정량의 분산 유도

이번에는 기댓값에 이어서 분산을 유도해보죠.

분산의 공식을 이용하여 다음을 전개해주면 식 (1)을 얻을 수 있습니다.

이때 위에서 언급한 것처럼 오차항만 확률적 요소라는 것만 기억하시면 됩니다.

식 (1)을 좀 더 세부적으로 살펴보죠.

 

E[∑wiei ]² 의 제곱식을 전개하면 위와 같습니다.

실제로는 행렬이 아니지만 이해하기 편하시라고 비슷하게 표현해보았습니다. (실제로는 덧셈으로 모두 연결되어 있습니다)

보시면 대각 성분은 w1e1, w2e2, w3e3, ... wnen 처럼 하첨자만 바뀌고 동일한 항이 계속 되는 걸 알 수 있으며,

대각 성분을 제외한 나머지 성분은 하첨자가 서로 같지 않은 성분에 대하여 대칭인 형태로 전개됨을 알 수 있습니다.

 

귀납적으로 한번 생각해보죠.

항이 2개(i = 1,2)만 있는 위 식의 괄호 항의 제곱식을 생각해보면 다음과 같습니다.

하첨자가 i=1, i=2인 성분에 대해서는 제곱식으로 표현되고,

하첨자가 서로 같지 않은 성분(i = 1 vs i = 2)에 대하여 대칭인 형태로 표현됨을 알 수 있죠.

 

이러한 성분이 이제 2개가 아닌 n개 있는 경우를 떠올려보면, 귀납적으로 충분히 보일 수 있습니다.

대각 성분은 (1)과 같이 쓸 수 있고, 대각 성분이 아닌 대칭인 성분은 (2)와 같이 쓸 수 있습니다.

 

이제 분산 유도식으로 돌아와서 다시 생각해보죠.

 

위 (1)식은 기댓값에 성질에 따라 두 기댓값의 합으로 분해할 수 있죠.

 

이때 단순회귀분석의 2가지 가정을 이용해보면,

1. 오차항의 공분산(Covariance)는 0이다.

2. 오차항의 분산은 상수 σ²이다.

이라고 할 수 있습니다.

 

다만 "1. 오차항의 공분산(Covariance)는 0이다"가 왜 (2)번과 같은지 모를 수 있는 분들을 위해 간단하게 정리하고 넘어가겠습니다.

 

어렵지 않죠?

 

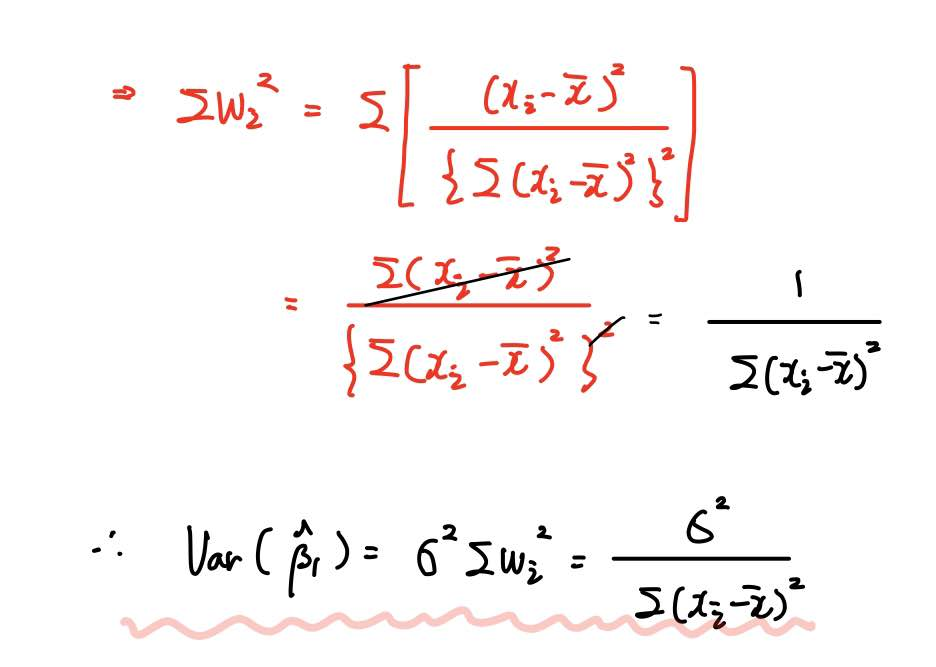
위 식에서 ∑wi²를 정리하면 위와 같이 됩니다.

따라서 β1 추정량의 분산은 위와 같이 정리할 수 있습니다.

 

 

이번 포스팅에서는 최소제곱추정량의 기댓값과 분산을 유도해보았습니다.

 

다음 포스팅에서는 β1의 최소제곱추정량이 가장 작은 분산을 갖는다는 점을 보이는 가우스-마르코프 정리를 다뤄보겠습니다.

 

 

감사합니다.

잘 읽으셨다면 게시글 하단에 ♡(좋아요) 눌러주시면 감사하겠습니다 :)

(구독이면 더욱 좋습니다 ^_^)

 

 

 

---

- 간토끼(DataLabbit)

- University of Seoul

- Economics, Big Data Analytics