[회귀분석] ANOVA(분산분석)를 이용한 회귀분석 접근 (3) - ANOVA Table 해석

Review

참고 포스팅 : 

2020/09/27 - [Statistics/Regression Analysis] - [회귀분석] ANOVA(분산분석)를 이용한 회귀분석 접근 (1) - 제곱합(Sum of Squares)

[회귀분석] ANOVA(분산분석)를 이용한 회귀분석 접근 (1) - 제곱합(Sum of Squares)

2020/09/29 - [Statistics/Regression Analysis] - [회귀분석] ANOVA(분산분석)를 이용한 회귀분석 접근 (2) - F ratio 유도

[회귀분석] ANOVA(분산분석)를 이용한 회귀분석 접근 (2) - F ratio 유도

---

안녕하십니까, 간토끼입니다.

 

ANOVA를 이용한 회귀분석 시리즈의 마지막 포스팅입니다.

 

지난 포스팅에서 다룬 내용을 정리하자면 먼저 반응변수 y를 설명 가능한 부분(y_hat)과 설명 불가능한 부분(error term)으로 나누어 이를 이용해 제곱합으로 표현했으며,

이 제곱합 간의 관계를 이용해 우리가 추정한 회귀식이 반응변수 y를 얼마나 잘 예측하고 설명하는지를 평가해야 한다고 했습니다.

이러한 모형 적합도의 평가를 위해 F-통계량을 사용해야 하는데 이 F-통계량이 어떠한 변수로부터 유도되는지를 2번째 포스팅에서 유도 과정을 중심으로 다뤄보았습니다.

 

이번 포스팅에서는 이렇게 유도한 F 값(통계량)을 해석하여 모형 적합도를 평가해보겠습니다.
(잘 모르시는 분들은 시리즈의 이전 포스팅을 다시 한번 보시기를 적극 권장합니다 ... ^^)

 

 

 

 

먼저 우리의 목적을 다시 한번 생각해보겠습니다.
바로 우리가 세운 회귀모형이 '통계적으로' 쓸모있는지, 즉 유의한 모형인지 살펴보는 게 목적이라고 했죠.

 

그래서 우리는 다음과 같은 가설을 검정해야 합니다.

 

 

 

회귀분석의 핵심은 설명변수 x와 반응변수 y 간의 관계를 찾아내는 것이라고 했습니다.

그렇기에 만약 기울기(Slope)가 0이라면 x와 y는 아무런 관계가 없다고 할 수 있겠죠?

 

이를 그래프로 나타내면 다음과 같습니다.

 

 

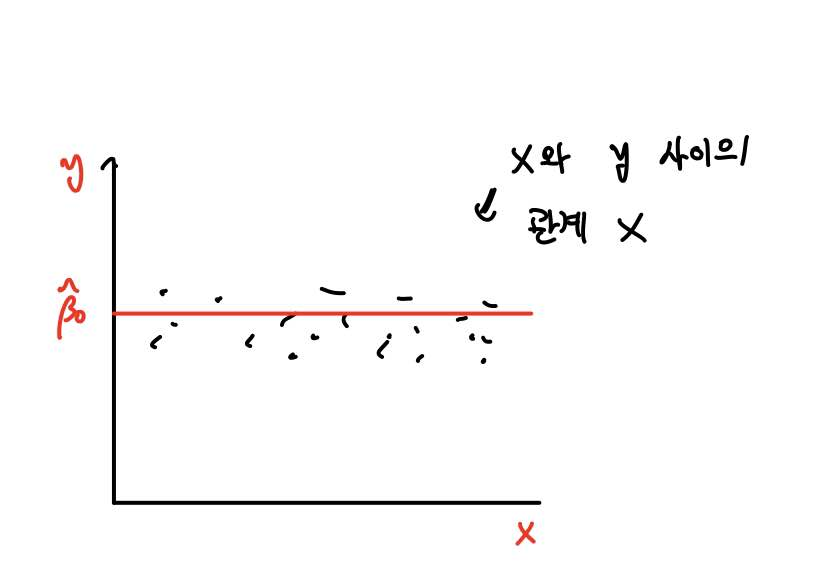
즉 기울기 계수  β1 = 0이 되면 단순회귀모형의 식은 y =  β0가 되니까,

상수항만 있는 함수의 형태는 위와 같습니다.

 

즉 설명변수 x와 반응변수 y 간 아무런 관계를 찾아볼 수 없게 됩니다.

왜냐하면 x가 아무리 커져도 y의 예측값은 변하지 않거든요.

(이것도 하나의 관계라면 관계라고 할 수 있겠네요...^^)

 

다만 이러한 형태의 모형은 우리가 굳이 추정할 필요는 없습니다.

왜냐하면 기울기가 없는 모형에서 상수항은 y의 평균을 의미하거든요.

 

그러니까 복잡하게 최소제곱추정량을 구할 필요없이 그냥 y의 평균만 구하면 된다는 말입니다.

 

 

자 그래서 우리는 회귀모형의 기울기 계수가 0인지 아닌지를 우선적으로 살펴봐야 합니다.

이러한 프로세스를 '가설 검정'이라고 하며, 우리가 검정하고자 하는 가설은 다음과 같습니다.

 

H0(귀무가설) : β1 = 0  ->  X와 Y는 아무런 관계가 없다!

H1(대립가설) : β1 ≠ 0  -> X와 Y는 어떠한 관계가 있다!

 

이때 핵심은 F-Test를 통해서는 모형의 기울기가 0인지 아닌지만 파악할 수 있고, 기울기가 0이 아니라면 양수인지 음수인지는 알 수 없다는 것입니다.

 

그럼 가설을 세웠으니 귀무가설 H0가 맞을지, 아니면 우리가 주장하고자 하는 대립가설 H1이 맞을지 검정해야겠죠?

 

이때 검정은 우리가 앞서 세운 검정통계량 F-ratio를 이용해,
유의수준 α에 따른 F분포의 임계값보다 큰지, 작은지를 따짐으로써 이뤄집니다.

 

 

 

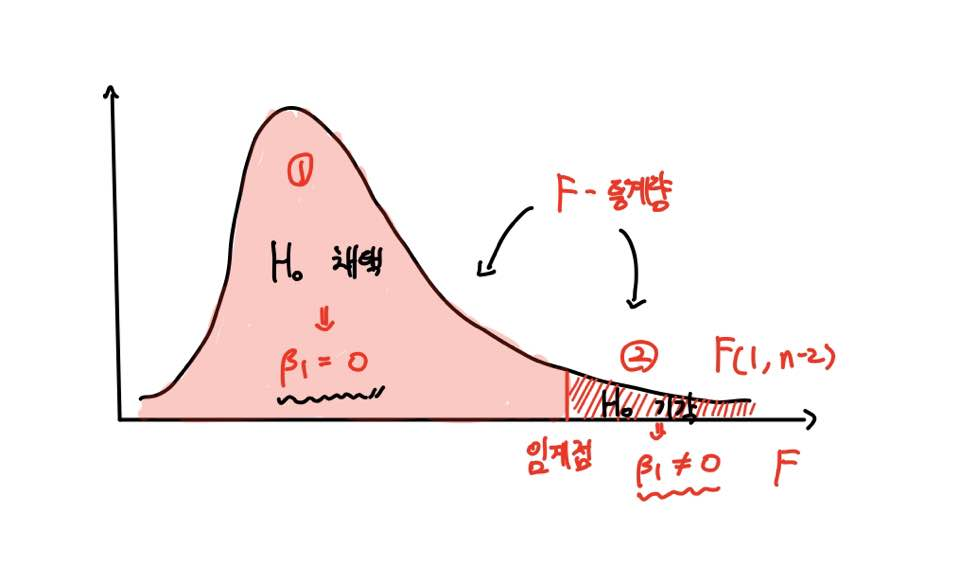
바로 위와 같은 F분포의 그래프에서 우리가 구한 검정통계량이 어디에 위치하는지에 따라 가설의 기각 여부가 결정됩니다.

 

이때 우리가 파악해야 할 것은 크게 2가지입니다.

1. 유의수준 α의 결정

2. 유의수준 α에 따른 기각역

 

가설검정을 다루는 파트는 아니니까, 이정도는 아신다고 가정하고 넘어가겠습니다.
(아직 포스팅하지는 않았지만, 추후 기초통계학에서 '가설검정'을 다루는 포스팅을 게시하면, 참고 링크를 남기겠습니다.)

 

먼저 F 통계량을 구해보겠습니다.

F-통계량은 다음 ANOVA Table에서 구할 수 있습니다.

 

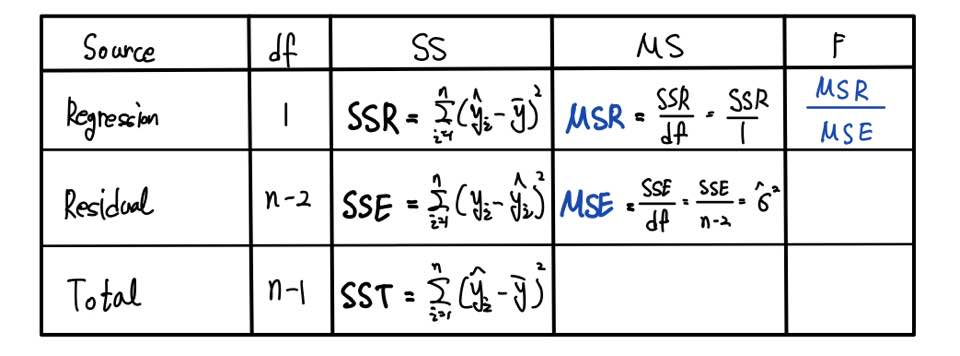
실제 계산을 손으로 하실 필요는 없고, data가 다 있으면 통계 프로그램이 구해서 알아서 출력해줍니다.

 

강조하자면 알아야 할 사항은 F-ratio = MSR/MSE 라는 것입니다.

이정도는 MSR과 MSE가 주어진다면 구할 수 있어야 합니다.

 

예시로 통계 프로그램 SPSS를 이용한 ANOVA Table의 출력 화면을 보시죠.

 

 

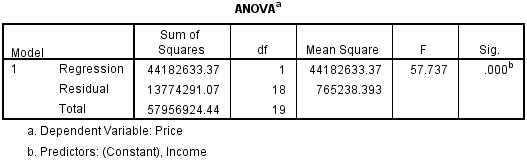
반응변수 y가 Price이고, 설명변수 x가 Income 인 단순회귀모형입니다.

 

이때 위 ANOVA Table을 참고하시면 MSR은 44182633.37 이고,

MSE는 765238.393 임을 쉽게 파악하실 수 있으실 겁니다.

 

이를 이용해 MSR / MSE 으로 F-통계량을 구해주면 57.737 이네요.

그리고 자유도가 (1, 18)이므로 위 F-통계량은 자유도가 (1,18)인 F-분포를 따른다고 볼 수 있습니다.

 

이때 유의수준 0.05 하에서의 임계값(Critical value)을 구해볼까요?

 

 

 

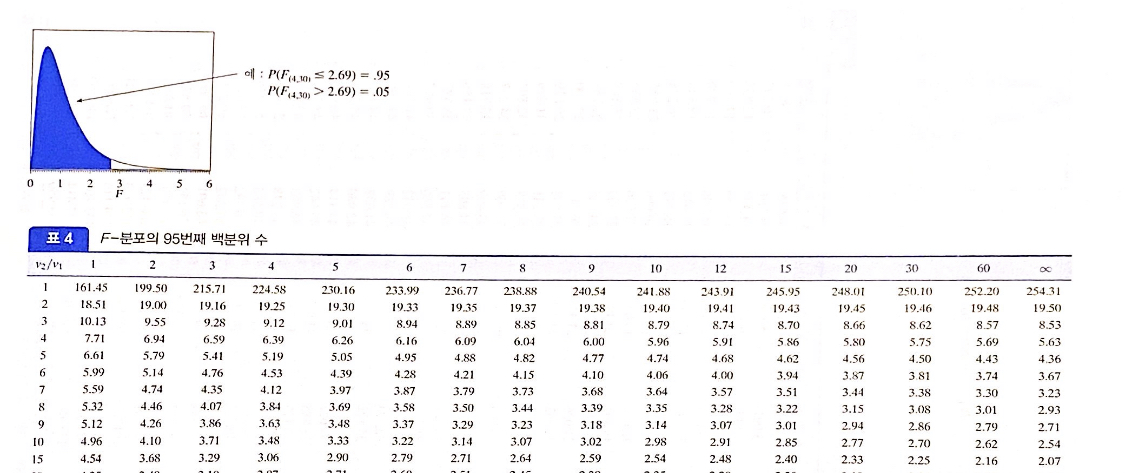
분포의 자유도가 (1, 18)이므로, v1 = 1 & v2 = 18인 부분을 찾으면 됩니다.

v2가 10, 15, 20 ... 이렇게 되어있어 18과 가까운 15 정도라고 가정하면 대략 4.54 정도 되겠군요!
(실제로는 자유도가 커질수록 F-분포의 값이 작아지고 있으니 4.54보다 작겠죠?)

 

그래서 임계값은 약 4.54라고 할 수 있습니다.따라서 우리가 구한 F-통계량이 4.54보다 크다면, 귀무가설 H0를 기각하여 대립가설 H1를 채택하는 것이고,
4.54보다 작다면 H1를 채택할 수 없게 됩니다.

즉 기울기가 0이라는 것이죠.

 

이때 위 ANOVA Table의 출력 화면을 보면 F-통계량이 57.737이죠?

임계값(Critical Value) 4.54보다 크니까 귀무가설 H0를 기각할 수 있습니다.

 

즉 회귀모형의 기울기가 0이 아니라는 결론을 내릴 수 있게 됩니다.

 

F-통계량 옆에 있는 숫자는 p-value(유의확률)이라고 부르는데요.

마찬가지로 아실 거라 생각하고 우선 넘어가겠으나, 핵심은 0에 가까울수록 통계적으로 유의하다고 합니다.

 

즉 우리가 세운 유의수준 α보다 p-value가 작으면 통계적으로 유의하다고 하고,
그렇지 않으면 통계적으로 유의하지 않다고 하며, 쉽게 말하면 결과를 신뢰할 수 없다는 얘기입니다.

 

즉 신뢰수준 95% (유의수준 α = 0.05) 하에서 위 결과는 통계적으로 유의하다고 결론을 내릴 수 있습니다.

 

 

다음 포스팅에서는 제곱합을 이용해 모형을 평가할 수 있는 지표인 결정계수(R-Squared)에 대해 다뤄보도록 하겠습니다.

 

감사합니다.

잘 읽으셨다면 게시글 하단에 ♡(좋아요) 눌러주시면 감사하겠습니다 :)

(구독이면 더욱 좋습니다 ^_^)

 

 

 

---

- 간토끼(DataLabbit)

- University of Seoul

- Economics, Big Data Analytics