[수리통계학] 확률변수의 변환(Transformation)

 

Review

참고 포스팅 :

2023.09.14 - [Statistics/Mathematical Statistics] - [수리통계학] 확률변수(Random Variable ; R.V.)

[수리통계학] 확률변수(Random Variable ; R.V.)

2023.10.05 - [Statistics/Mathematical Statistics] - [수리통계학] 이산확률변수와 연속확률변수(Discrete and Continuous Random Variable)

[수리통계학] 이산확률변수와 연속확률변수(Discrete and Continuous Random Variable)

# 해당 포스팅은 KOCW 김충락 교수님의 수리통계학 강의와 Hogg의 수리통계학개론(Introduction to Mathematical Statistics)를 기초로 작성되었습니다.

---

안녕하십니까, 간토끼입니다.

이번 포스팅에서는 확률변수 X의 분포를 알고 있을 때 X와 연관된 확률변수 Y = g(X)의 분포를 구할 수 있는 개념인 변환(Transformation)에 대해 다뤄보겠습니다.

 

---

우리는 확률변수의 누적분포함수(CDF)와 확률밀도함수(PDF)를 알고 있다면, 이 확률변수의 분포를 알고 있다고 합니다.

 
분포를 알고 있는 것은 매우 중요합니다.
지피지기면 백전백승이라고, 확률변수 $X$의 각 원소에 대해 발생 확률을 구할 수 있다는 것이죠.

상자 안에 빨간색, 녹색, 파란색(R,G,B) 공이 담겨 있고, 이 상자에서 공을 하나 뽑는 상황을 가정합시다.
그리고 확률변수 $X$를 뽑은 공의 색깔이라고 합시다.
 
만약 우리가 상자 안의 공의 분포에 대해서 알지 못한다면, $X$를 예상하는 것은 그저 찍기에 불과할 것입니다.

하지만 우리가 R,G,B의 분포가 각각 (0.2, 0.5, 0.3) 이라는 것을 알고 있다면
확률적이지만 "초록색"에 배팅하는 것은 꽤나 합리적인 결정이라고 볼 수 있죠.

간단한 예시였지만 확률변수의 분포를 아는 것은 꽤나 중요하다는 것을 강조하고 싶었습니다.
분포를 알고 있다면 이 분포를 바탕으로 확률변수가 특정 값으로 주어졌을 때의 결과를 예측 할 수 있기 때문이죠.
 

만약 확률변수 $X$의 분포를 알고 있을 때, 새로운 확률변수 $Y$가 등장한다면 어떻게 될까요?

이 $Y$는 $X$와 관계가 있는, 즉 함수 $g(x)$ 꼴로 표현되는 확률변수라고 가정합시다.
이 $g(x)$를 알고 있다면 우리는 $X$로부터 $Y$의 확률분포를 구할 수 있을까요?

이를 변환(Transformation)이라고 합니다.
이번 포스팅에서는 이 변환에 대해 다뤄보겠습니다.
 
지난 포스팅에서 다룬 바와 같이 확률변수를 이산형이냐, 연속형이냐에 따라 구분하여 변환하는 방법을 다뤄보겠습니다.

728x90

 
 
1. 이산확률변수의 변환

확률변수 $X$를 공간 $D_x$를 가진 이산확률변수라고 합시다.
이때 새로운 확률변수 $Y$는 $Y=g(X)$ 꼴로 표현되는 변수이고, 마찬가지로 확률변수이므로 공간 $D_y$를 갖습니다.
 

변환함수 $g$가 일대일 대응 함수라고 가정해보겠습니다.
일대일 대응 함수라는 것은 역함수가 존재한다는 것과 같은 의미죠.

$g(x)=y$에서 $g$의 역함수를 구하면 $x=g^{-1}(y)$가 됩니다. 이를 기존 확률변수의 pdf에 대입해주면 끝입니다. 쉽죠?

위 전개 과정을 보시면 금방 이해가 되실 겁니다.

 
예를 한번 보시죠.

지난 포스팅에서 다루었던 예시죠.

확률변수 X를 동전을 던졌을 때 '첫번째로 앞면(H)이 나올 때까지 던진 동전의 총 횟수'라고 정의하겠습니다.
그러면 확률질량함수는 $(\frac{1}{2}{)}^x$ 가 되겠죠.
 
이때 새로운 확률변수 $Y$를 '첫번째로 앞면(H)이 나오기 전까지 던진 동전의 총 횟수'라고 해봅시다.
'나오기 전까지' 이므로 X에서 1을 빼면 되겠죠. $Y=X-1$ 로 표현할 수 있겠습니다.

그러면 $g(x)=X-1$ 이니까 일대일대응이고, 역함수는 $X=Y+1$이겠네요.
이를 기존 확률질량함수 $P_x$에 대입해주면 $(\frac{1}{2}{)}^{y+1}$이 되겠네요. 쉽죠?
 

만약 변환함수 $g$가 일대일 대응이 아니라면 어떻게 해야할까요?

답은 각 이산적인 값에 따라 일일이 pmf를 구해줘야 합니다.
크게 어려운 부분은 아니니 오늘 포스팅의 핵심인 연속확률변수로 넘어가겠습니다.
 

---

 
2. 연속확률변수의 변환

확률변수 $X$를 pdf $f_x$와 support $S_x$를 가진 연속확률변수로 가정하겠습니다.
그리고 위와 마찬가지로 새로운 확률변수 $Y$는 변환함수 $g(x)$를 통해 정의되는 변수고, 변환함수 $g$는 일대일대응이며 미분 가능한 함수라고 정의하겠습니다.
 
연속확률변수의 변환 방법은 크게 두 가지가 있는데요.

첫 번째는 누적분포함수(CDF)를 활용한 기법이고, 두 번째는 자코비안 행렬을 활용한 기법입니다.
하나씩 다뤄보죠.

 
(1) CDF Technique

CDF 기법은 새로운 확률변수 $Y$의 CDF를 구하고, CDF의 미분은 pdf임을 이용하여 $Y$의 pdf를 구하는 기법입니다.

먼저 변환함수 $g$의 역함수를 구하고, 새로운 확률변수 $Y$의 cdf를 도출합니다.
cdf의 정의에 따라 $F(y)=P(g(x)\le y)$로 표현할 수 있습니다.
 
이때 g의 역함수를 활용하면
$$=P(g(x)\le y)=P(X\le g^{-1}(y))=F_X(g^{-1}(y))$$
여기서 $P(X\le g^{-1}(y))$ 은 확률변수 $X$에 대한 식입니다.
그리고 $X$의 cdf와 같으므로 $F_X$로 쓸 수 있습니다.
즉 기존 확률변수의 cdf를 이용할 수 있다는 거죠.

 
그러면 이를 미분하여 새로운 확률변수 $Y$의 pdf를 도출할 수 있습니다.
$$cdf:f_Y(y)=\frac{\mathrm{d}}{\mathrm{d}x}{F}_X(g^{-1}(y))$$
 
쉬운 예시를 통해 직관적으로 이해해봅시다.
 

 
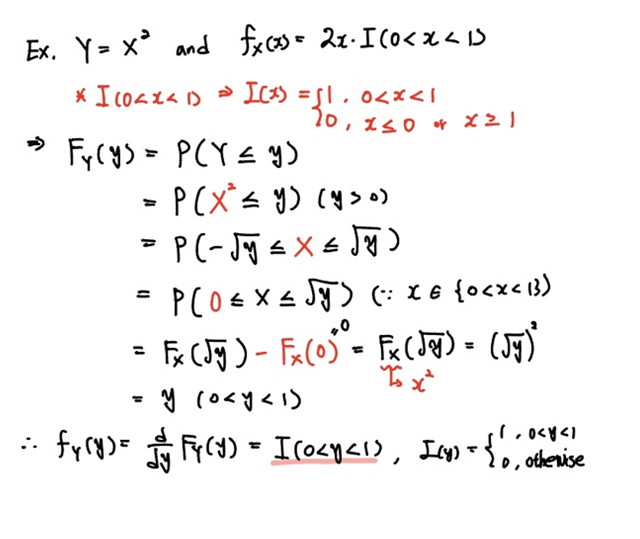
확률변수 $X$의 pdf가 $2x$이고, x의 support $S_x$는 0부터 1까지의 구간이라고 합시다.
그리고 새로운 확률변수 $Y=X^2$ 의 관계를 통해 확률변수 Y가 정의되었다고 가정합시다.

새로운 표기법이 하나 등장하는데요.
$I(·)$ 는 지시함수(Indication Function)이라고 합니다. 특정 조건을 만족하면 1이고, 그렇지 않으면 0으로 표기합니다.

즉 확률변수 $X$의 support이면 1이고, support가 아니라면 0이라는 것과 동일한 의미겠죠. 앞으로 자주 등장하는 표현입니다.
 
위에서 다루었던 CDF 기법의 절차대로 풀어내면 새로운 확률변수 $Y$의 pdf는 $I(y)$이고, $Y$의 support는 x와 마찬가지로 0부터 1 사이의 구간입니다.
이 구간에 해당되면 1이고, 그렇지 않으면 0입니다.

 
2. Jacobian Technique

Jacobian 기법은 말 그대로 Jacobian Matrix(자코비안 행렬)의 행렬식(Determinant)을 이용하여 새로운 확률변수 $Y$의 pdf를 구하는 기법입니다.

Jacobian은 자코비안이라고도 하고, 제이코비안이라고도 하고, 야코비안이라고도 하는데 저는 자코비안이라고 하겠습니다. 발음이 더 편해서요. 그렇지 않나요? ㅎㅎ

절차는 보시는 바와 같습니다.
변환함수 $g$의 역함수 $g^{-1}$와, 이에 대한 Jacobian을 구해서 기존 확률변수의 pdf에 역함수를 대입하고, Jacobian을 이 pdf에 곱해주기만 하면 끝입니다!
 
위 변환된 식의 도출 과정을 한번 보여드리겠습니다.

먼저 변환함수 $g$를 단조증가함수로 가정하겠습니다. 일대일 대응이기 때문이죠.
물론 일대일 대응이기 때문에 단조증가 혹은 단조감수 형태일 겁니다. 먼저 단조증가의 case에 대해 다뤄보겠습니다.

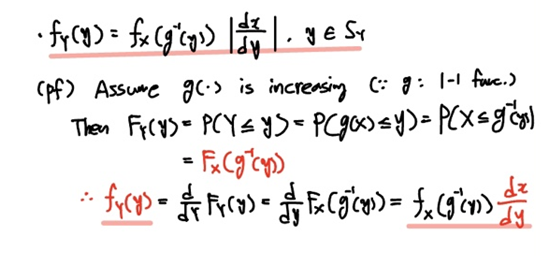
크게 어려운 부분은 없습니다.

위에서 다뤘던 내용에서 크게 벗어나지는 않거든요.
다만 기존 확률변수의 cdf를 y에 대해 미분하는 과정에서 Jacobian이 등장하게 됩니다.

등장하는 이유는 기존 확률변수의 cdf는 X에 대한 함수고, y에 대해 미분할 때 chain rule을 적용하니 튀어나오는 거죠.

 
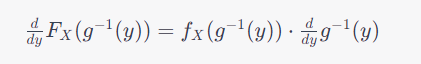
수리통계학을 공부하시는 분들이라면 Jacobian의 개념도 아실 거라 생각하지만, 간단하게 소개하고 넘어가겠습니다.

자코비안 행렬은 다변수 함수에서 편미분한 값들을 모아놓은 행렬입니다.
만약 종속변수 Y가 $y_1,y_2$ 이고, 각 종속변수는 2개의 독립변수 $x_1,x_2$에 대해 표현되는 다변수 함수라고 합시다.

그러면 각 독립변수에 대해 미분하면 총 4개의 1계 미분한 결과가 나오겠죠.
이를 행렬의 형태로 표현하면 Jacobian이 됩니다. 그리고 Jacobian의 각 column은 그레디언트 벡터에 해당합니다.
미적분 세션은 아니니까 이정도로 넘어가겠습니다.
 

만약 $g$가 단조감소형태라면 다음과 같은 전개 과정을 거치지만 결국 결과는 같습니다.

김충락 교수님의 강의자료에서 발췌

 
CDF 테크닉에서 다루었던 예시를 Jacobian을 이용해 동일한 결과가 도출되는지 보겠습니다.

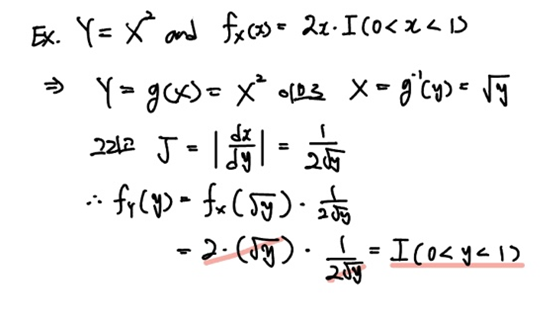
마찬가지로 새로운 확률변수 $Y$의 pdf는 Indication function인 $I(y)$가 도출됨을 알 수 있습니다.

결과는 같네요. 그렇다면 왜 서로 다른 기법을 사용해야 할까요?
 
사실 Jacobian 기법은 일변수 함수의 변환에서는 유용한 기법은 아닙니다.
말 그대로 Jacobian을 활용하는 만큼, 다변수 함수에서의 변환에서 강점을 가지죠.

만약 다변수 함수의 변환이라면 도출된 Jacobian의 Determinant를 구해서 절댓값을 취한 후 곱해주시면 됩니다.
이는 Determinant가 음수가 되는 것을 방지하고자 절댓값을 취하는 것이니 인지해주시면 되겠습니다.

이후 포스팅에서는 다변수 확률분포도 나오는 만큼, 이때 Jacobian Technique이 많이 쓰일 겁니다.

즉, 상황에 따라 유용한 기법을 사용하면 되겠습니다.
 

다음 포스팅에서는 확률변수 파트에서 매우 매우 중요한 기댓값(Expectation)에 대해 다뤄보겠습니다.

 
감사합니다.

잘 읽으셨다면 게시글 하단에 ♡(좋아요) 눌러주시면 감사하겠습니다 :)
(구독이면 더욱 좋습니다 ^_^)

* 본 블로그는 학부생이 운영하는 블로그입니다.
따라서 포스팅에 학문적 오류가 있을 수 있으며, 이를 감안해서 봐주시면 감사하겠습니다.
 

---

- 간토끼(DataLabbit)
- B.A. in Economics, Data Science at University of Seoul